Системы разностных уравнений

Этот класс моделей описывает детерминированные системы с непрерывным состоянием и дискретным временем перехода. Если интервалы между моментами перехода равны, то удобно пронумеровать рассматриваемые моменты времени, и тогда такую систему можно записать в следующем общем виде 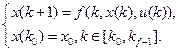– уравнение состояния, (6)

– уравнение выхода. (7)

Соответственно для линейных систем:

A(k) – переходная матрица состояний на 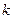– ом шаге вычисления решения.

Уравнение с дискретным временем может, например, быть применено в случаях, когда измерения и воздействия на непрерывную систему осуществляются в дискретные моменты времени. Если принять интервал дискретности равным 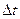, то можно в соответствии с (5) записать для линейной непрерывной системы:

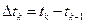; . (8)

Если принять на интервале постоянным и равным 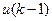, то можно (8) представить в виде

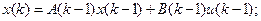(9)

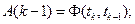
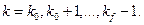
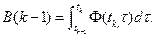(10)

3.1.3. Примеры систем, описываемых в классе D – схем

Обыкновенными дифференциальными и разностными уравнениями хорошо описывается поведение широкого класса объектов и систем различной физической природы с непрерывным или дискретным временем и непрерывным состоянием. Прежде всего, следует отметить объекты, объединяемые общим определением – «емкости». Это пневматические, гидравлические, тепловые, электрические системы.

Общий вид уравнений, описывающих динамику изменения состояния таких систем

(11)

где - скорость изменения состояния, и 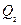- приток и соответственно отток

энергии, теплоты, вещества в единицу времени.

Для пневматической емкости при постоянном объеме можно записать:

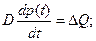(12)

–переменная состояния – давление в емкости;

изменение количества тепла в единицу времени;

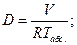
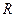- универсальная газовая постоянная; – объем емкости.

Для гидравлической емкости состоянием является – объем жидкости в емкости;

, (13)

- изменения количества жидкости в единицу времени;

- удельный вес жидкости.

Для тепловой емкости изменение температуры вещества определяется уравнением

; (14)

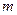–масса тела, – удельная теплоемкость, – изменение количества теплоты в единицу времени.

Уравнение движения материальной точки в трехмерном пространстве описывается уравнениями (второй закон Ньютона):

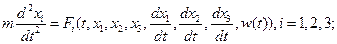или

; (15)

где 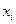, =1,2,3 – координаты точки – составляющие вектора состояния ; , 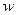– функция воздействий на объект.

Для химического реактора, в работе которого участвует веществ, если составляющая вектора состояния - концентрация – го вещества; уравнения состояний можно принять в виде:

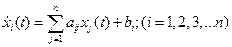; ( =1,2,…, ). (16)

Экологическая система, переменные вектора состояний 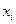, =1,2,…, которой представляют собой размер i-ой популяции; уравнения состояний имеют вид:

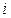; ( = 1,2,…, ); (17)

Примером описания объекта в дискретной по времени форме системой разностных уравнения может служить, например, математическая модель межотраслевых связей «затраты – выпуск» экономической системы. Если 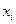– валовой выпуск – го продукта (в стоимостном выражении) в единицу времени; - количество – го продукта, потребляемого для изготовления 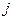– го продукта, условие самообеспечения экономики имеет вид:

(18)

или, при наличии дополнительных инвестиций,

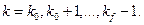; (19)

Дата добавления: 2014-12-27