Марковские процессы с непрерывным временем. Дифференциальные уравнения относительно вероятностей состояний

Если система может находиться в одном из счетного множества состояний и переход из состояния в состояние происходит в любой момент времени, определяемый простейшими случайными потоками событий, процесс изменения состояния такой системы во времени является марковским процессом с дискретным состоянием и непрерывным временем.

Известно [7], что различные характеристики поведения систем, процесс функционирования которых представляет собой марковский случайный процесс с дискретным состоянием и непрерывным временем, могут быть получены, если известны вероятности пребывания системы в тех или иных состояниях для любых рассматриваемых моментов времени. Эти вероятности определяются решением системы линейных дифференциальных уравнений, которые имеют при определенных условиях (стационарность и эргодичность процесса) установившиеся или так называемые финитные решения (при t 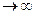), не зависящие от начальных условий. Обычно эти финитные вероятности и определяют основные показатели эффективности систем.

Так для СМО с отказами одной из важнейших характеристик является так называемая абсолютная пропускная способность – среднее число заявок, обслуживаемое за единицу времени. Рассматривается также относительная пропускная способность – отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступивших за это время заявок. В зависимости от задачи исследования могут определяться и такие показатели, как среднее число занятых каналов, среднее относительное время простоя системы в целом и отдельного канала. Для СМО с ожиданием и смешанного типа весьма важными характеристиками являются среднее число заявок в очереди, среднее число заявок в системе (в очереди и на обслуживании), среднее время ожидания заявки в очереди, среднее время пребывания заявки в системе (в очереди и на обслуживании).

В связи с этим соотношения, определяющие эти характеристики, и, прежде всего сами дифференциальные уравнения относительно вероятностей состояний и представляют собой аналитическую модель рассматриваемой системы. Эти дифференциальные уравнения, называемые уравнениями Колмогорова, могут быть получены из разностных уравнений для вероятностей состояний систем с дискретным временем.

Пусть - вероятность того, что в момент t система находится в состоянии i, i=1,2,…,n;

и - интенсивность потока событий, переводящего систему из состояния i в состояние j.

Марковский процесс перехода системы из состояния в состояние с непрерывным временем перехода вызывается пуассоновским потоком.

Пуассоновский поток – это ординарный поток без последействия.

Ординарность позволяет считать, что

(10)

где 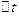- малое (по крайней мере, по сравнению с величиной 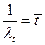) приращение текущего времени t;

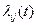- плотность потока событий, вызывающих переход из состояния i в состояние j.

Отсутствие последействия позволяет при моделировании не учитывать, сколько

времени система находилась в некотором состоянии для определения момента времени

очередного перехода, т.к. оставшееся до момента перехода время распределено по тому же закону, что и длительность интервалов между событиями, вызывающими переход.

Эти свойства определяют возможность составления систем линейных дифференциальных уравнений относительно вероятностей нахождения системы (или процесса) в том или ином состоянии.

Действительно, подставив (10) в (9) в случае пуассоновского потока событий получим:

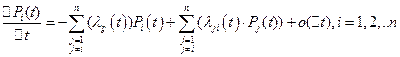
Устремляя 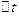к нулю, перейдем к системе дифференциальных уравнений:

(11)

Если потоки событий ещё и стационарны, имеют место простейшие потоки, интенсивности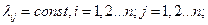

В этом случае (как и в случае процессов с дискретным временем) в системе (1),

независимо от начальных условий могут иметь место установившиеся решения, т.е. значения .

Эти решения во многих практических случаях и являются основными данными для оценки качества функционирования таких систем.

Подобно тому, как в случае дискретного времени перехода, когда процесс задается матрицей переходных вероятностей, в случае непрерывного времени марковский процесс задается матрицей соответствующих переходных интенсивностей, где диагональные элементы могут не задаваться.

И в том, и в другом случае, процесс может быть представлен в виде графа, вершины которого отображают состояния, а дуги размечены либо переходными вероятностями , либо соответствующими интенсивностями потоков переходов 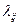(интенсивностями потоков, вызывающих i®j переход).

Из приведенного выше следует, что если мы имеем дело с марковским процессом и если он задан интенсивностью потока переходов (и, естественно, начальным состоянием), то, задаваясь достаточно мелким шагом, скажем, на 1-2 порядка меньше минимального (10): значения 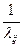, его можно задать матрицей переходных вероятностей, применяя

(12)

т.е. процесс с непрерывным временем представить как процесс с дискретным временем (и тот, и другой с дискретными состояниями). Соответственно, можно сделать и обратный переход, если каждому такту определения очередного состояния по жребию придать смысл вероятностного интервала.

Рассмотрим процесс с двумя возможными состояниями х=1 и х=2.

Дано: l12=1/20; l21=1/15; т.е. – поток простейший.

При 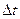= 0.5 Р12 = 0.025, Р11 = 0.975, Р21 = 0.033, Р22 = 0.967.

Примем 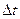= 1. Тогда Р12 = 0.050, Р11 = 0.95, Р21 = 0.063, Р22 = 0.937.

	—	l12
	l21	—

	0.95	0.05
	0.063	0.937

Очевидно, чем больше lij, тем меньше среднее значение интервалов между событиями и тем больше вероятность перейти из состояния 1 в состояние 2 (или из 2 в 1) за промежуток времени Dt. Возникает возможность моделирования реализации одного и того же марковского процесса по двум подходам к продвижению модельного времени:

1. по особым состояниям;

2. по принципу Dt – продвижения на заданный шаг.

В первом из них с использованием датчика случайных чисел формируются интервалы между событиями (т.е. моментами перехода) 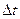=exprnd(); принимается t=t+ , где – минимальный по всем j из интервалов при переходе из i – го состояния в j – ое.

Во втором - Dt=const и t=t+ 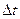. Используется обращение к датчику случайных чисел равномерно распределенных в [0;1] и выбор очередного события по жребию. В этом подходе события – это остаться в прежнем состоянии или перейти в другое, выбранное по жребию.

Структура дифференциальных уравнений определяется следующим правилом их составления.

В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок на графе связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак минус; если в состояние – знак плюс. Каждый член равен произведению плотности вероятности перехода (интенсивности потока событий), соответствующей данной стрелке, и вероятности того состояния, из которого исходит стрелка.

Финитные вероятности могут быть получены из решения системы алгебраических уравнений, следующих из (1), если положить:

и .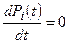

Для многих, часто встречающихся форм графов переходов, линейные алгебраические уравнения для финитных вероятностей имеют довольно простое аналитическое выражение.

Для такого рода систем естественно в качестве типовой математической схемы при построении модели использовать марковские процессы и, в частности, однородные марковские цепи, или в более широком плане схемы вероятностных автоматов – .

Дата добавления: 2014-12-27