
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Непрерывно-стохастическая модель. Потоки случайных событий
|
|
|
|
В системах, которые могут быть описаны в классе 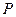 - схем, обычно принимают, что переход из состояния в состояние совершается мгновенно, а время перехода связывают с тем, что происходит некоторое событие, которое и определяет момент перехода, а часто и входной сигнал. Последовательность таких событий, происходящих одно за другим в случайные, заранее не известные моменты времени, называют потоком случайных событий. Этот поток определяет получаемую последовательность состояний системы во времени. Если эти состояния случайны, то говорят, что в физической системе происходит случайный или вероятностный процесс с непрерывным временем и дискретным состоянием.
- схем, обычно принимают, что переход из состояния в состояние совершается мгновенно, а время перехода связывают с тем, что происходит некоторое событие, которое и определяет момент перехода, а часто и входной сигнал. Последовательность таких событий, происходящих одно за другим в случайные, заранее не известные моменты времени, называют потоком случайных событий. Этот поток определяет получаемую последовательность состояний системы во времени. Если эти состояния случайны, то говорят, что в физической системе происходит случайный или вероятностный процесс с непрерывным временем и дискретным состоянием.
Примерами потоков являются, например, поток обращений к сайту, поток машин на заправку, поток заявок на выполнение тех или иных работ и т.д.
Поток событий называется однородным, если он характеризуется только моментами наступления событий (вызывающие моменты) и задается последовательностью:
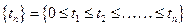 (1),
(1),
где 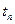 – момент наступления n-ого события – неотрицательное вещественное число.
– момент наступления n-ого события – неотрицательное вещественное число.
Например, если в соответствии с поставленной задачей не требуется различать типы самолетов, приземляющихся в аэропорту, то поток событий приземления можно рассматривать как однородный.
Однородный поток может так же быть задан в виде последовательности промежутков между n-м и (n-1)-м событиями 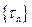 , которые однозначно связаны с последовательностью вызывающих моментов
, которые однозначно связаны с последовательностью вызывающих моментов 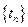
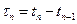 ;
; 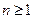 ,
, 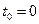 ,
, 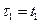 .
.
Последовательность 
 - последовательность случайных положительных (неотрицательных) чисел.
- последовательность случайных положительных (неотрицательных) чисел.
Потоком неоднородных событий называется последовательность 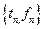 , где
, где 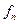 - набор признаков события (например, тип самолета).
- набор признаков события (например, тип самолета).
Если интервалы  ;
; 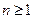 независимые случайные числа – поток событий называют потоком с ограниченным последействием, или потоком Пальма.
независимые случайные числа – поток событий называют потоком с ограниченным последействием, или потоком Пальма.
Поток событий называется ординарным, если вероятность того, что на малый интервал времени 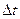 , примыкающий к моменту t, попадает больше одного события, пренебрежимо мала по сравнению с вероятностью того, что на этот же интервал времени
, примыкающий к моменту t, попадает больше одного события, пренебрежимо мала по сравнению с вероятностью того, что на этот же интервал времени 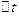 попадет не более одного события.
попадет не более одного события.
Пусть вероятности 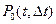 ,
, 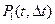 ,
, 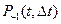 есть вероятности того, что на интервал
есть вероятности того, что на интервал 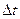 соответственно событие не попадает, попадает ровно одно событие и попадает более одного события. Это вероятности полной группы несовместных событий. Тогда для ординарного потока можно записать:
соответственно событие не попадает, попадает ровно одно событие и попадает более одного события. Это вероятности полной группы несовместных событий. Тогда для ординарного потока можно записать:
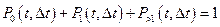 ; (2)
; (2)
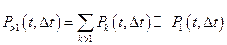 ; (3)
; (3)
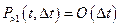 ; (4)
; (4)
где 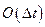 - величина порядка малости, выше
- величина порядка малости, выше 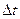 т.е.
т.е.
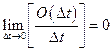 . (5)
. (5)
Среднее число событий на интервале 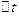 есть:
есть:
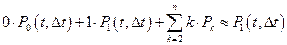 ; (6)
; (6)
т.е. 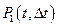 при малых
при малых 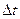 численно равно среднему числу событий на интервале.
численно равно среднему числу событий на интервале.
Для ординарного потока событий:
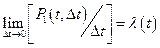 , (7)
, (7)
(если этот предел существует);
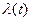 называется интенсивностью (плотностью) потока. Физически
называется интенсивностью (плотностью) потока. Физически 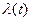 среднее число событий в единицу времени. Это неотрицательная функция времени, имеющая размерность
среднее число событий в единицу времени. Это неотрицательная функция времени, имеющая размерность 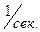 .
.
Стационарным потоком событий называется поток, для которого вероятность появления некоторого числа событий на интервале, длинной 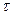 , зависит лишь от длинны интервала и не зависит от того, где на оси времени взят этот интервал. Для такого потока l=const. (не зависит от времени). Экспериментальной оценкой плотности потока может служить отношение
, зависит лишь от длинны интервала и не зависит от того, где на оси времени взят этот интервал. Для такого потока l=const. (не зависит от времени). Экспериментальной оценкой плотности потока может служить отношение
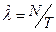 ,
,
где 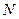 - число событий,
- число событий, 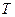 - интервал времени.
- интервал времени.
Если вероятность наступления 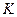 событий в полуинтервале
событий в полуинтервале 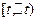 не зависит от того, сколько событий наступило в интервале [
не зависит от того, сколько событий наступило в интервале [ 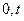 ), то поток называют потоком без последействия (с отсутствием последействия).
), то поток называют потоком без последействия (с отсутствием последействия).
Простейшим потоком называют стационарный, ординарный поток без последействия.
Пуассоновский поток событий - это ординарный поток без последействия.
Если на числовой оси взять два интервала длинной 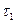 и
и 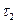 ,
, 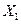 и
и 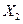 - числа событий на соответствующих интервалах, то для потока без последействия числа
- числа событий на соответствующих интервалах, то для потока без последействия числа 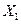 и
и 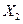 являются независимыми случайными числами и
являются независимыми случайными числами и 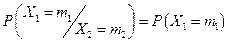 ; где
; где 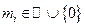 . Т.е. условная вероятность того, что
. Т.е. условная вероятность того, что 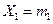 при условии
при условии  равна безусловной вероятности того, что
равна безусловной вероятности того, что 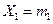 .
.
Пусть 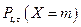 - вероятность того, что на отрезке длиной t с началом в момент времени
- вероятность того, что на отрезке длиной t с началом в момент времени 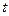 произойдет число событий
произойдет число событий  =
= 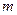 . Эта вероятность для пуассоновского потока событий определяется соотношением:
. Эта вероятность для пуассоновского потока событий определяется соотношением:
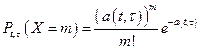 ; (8)
; (8)
где a(t,t)- среднее число событий на рассматриваемом интервале.
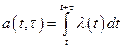 . (9)
. (9)
Если пуассоновский поток – стационарный, то
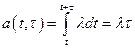 ; (10)
; (10)
и на участке длительностью t наступит m событий с вероятностью:
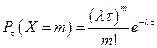 ; (11)
; (11)
т.е. простейший поток- это стационарный пуассоновский поток.
Найдем закон распределения интервалов времени 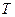 между двумя соседними состояниями.
между двумя соседними состояниями.
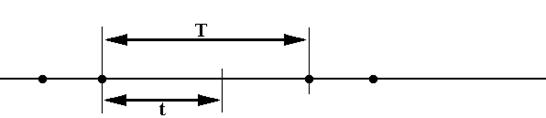
Рис. 1
Вероятность того, что на участке t не будет ни одного события:
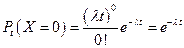 ; (12)
; (12)
но 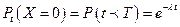 .
.
Тогда функция распределения 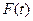 интервалов времени
интервалов времени 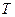 между событиями будет равна:
между событиями будет равна:
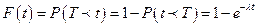 ; (
; (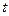 >0); (13)
>0); (13)
а плотность распределения имеет вид:
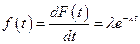 . (14)
. (14)
Таким образом, интервалы времени между событиями в простейшем потоке распределены по закону (14), называемому экспоненциальным или показательным законом плотности распределения вероятностей.
Математическое ожидание и дисперсия интервалов 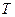 определяются соотношениями:
определяются соотношениями:
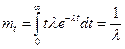 ; (15)
; (15)
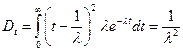 (16)
(16)
Если интенсивность высока, то 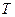 мало. Вообще говоря, если интервалы распределены по одному и тому же закону f(z), поток называют рекуррентным и среднее значение интервала определяется обычной формулой математического ожидания:
мало. Вообще говоря, если интервалы распределены по одному и тому же закону f(z), поток называют рекуррентным и среднее значение интервала определяется обычной формулой математического ожидания:
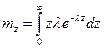 .
.  (17)
(17)
Используются и другие виды потоков, например регулярный поток, т.е. поток, в котором моменты времени появления событий заранее определены, или потоки Эрланга различных порядков, формируемые на основе “просеивания” простейших потоков.
 |
Так, поток Эрланга к - го порядка 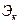 – это поток, интервалы между событиями в котором составляют сумму k+1-ой независимых случайных величин, распределенных по показательному закону. Поток
– это поток, интервалы между событиями в котором составляют сумму k+1-ой независимых случайных величин, распределенных по показательному закону. Поток 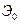 есть простейший поток. Потоки Эрланга являются стационарными ординарными потоками с ограниченным последействием.
есть простейший поток. Потоки Эрланга являются стационарными ординарными потоками с ограниченным последействием.
Главной характеристикой случайного потока является его интенсивность – своеобразная «скорость» появления событий.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 860; Нарушение авторских прав?; Мы поможем в написании вашей работы!