Дискретно-детерминированная модель. Конечные автоматы

Автомат – это некоторое устройство, на которое подаются входные сигналы и снимаются выходные сигналы и которое может иметь некоторые внутренние состояния.

Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а, следовательно, и множество выходных сигналов) являются конечными множествами.

Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами:

· конечным множеством входных сигналов (входным алфавитом);

· конечным множеством выходных сигналов (выходным алфавитом);

· конечным множеством внутренних состояний (внутренним алфавитом или алфавитом состояний);

· начальным состоянием ;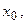

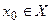· функцией переходов ;

· функцией выходов .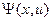

Автомат, задаваемый

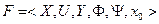(1) функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, входной и выходной сигналы, соответствующие такту при 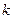=0,1,2…,через x(k), u(k), y(k). При этом , , .

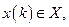
Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент 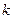=0,1,2… дискретного времени автомат находится в определенном состоянии x(k) из множества состояний автомата. В начальный момент k=0 он всегда находится в начальном состоянии . В момент 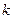, будучи в состоянии x(k), автомат способен воспринять на входном канале сигнал и выдать на выходной канал сигнал

, (2)

переходя при этом в следующий момент дискретного времени 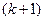в состояние

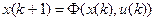, , . (3)

Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита во множество слов выходного алфавита.

Таким образом, работа конечного автомата происходит по следующей схеме: в каждом k – ом такте на вход автомата, находящегося в состоянии x(k), подается некоторый сигнал u(k), на который он реагирует переходом в (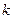 +1) – ом такте в новое состояние и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями:

для F-автомата первого рода, называемого также автоматом Мили

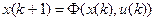, (4)

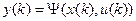, (5)

для F-автомата второго рода:

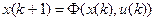, (6)

, (7)

Автомат второго рода, для которого 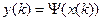, 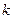=0,1,2…, т.е. функция выходов не зависит от входной переменной u(k), называется автоматом Мура.

В зависимости от мощности множеств 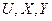и вида функций и различают следующие виды автоматов.

1. Автомат без памяти (комбинационная схема). В этом случае множество состояний имеет лишь один элемент, т.е. автомат есть тройка 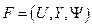. Рекуррентные соотношения (2) и (3) вырождаются в логическую функцию

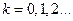; . (6)

Это булева функция, если алфавиты и состоят из двух букв.

Если множество состояний содержит более одного элемента автомат определяют как автомат с памятью.

2. Автономный автомат. Множество входных сигналов состоит из одного элемента, что означает неизменность входа. Автомат определяется четверкой и соотношения (2),(3) принимают вид

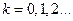; . (7)

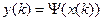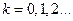; . (8)

Здесь состояние и выход зависят только от состояния и не зависят от входа. Автомат функционирует автономно, т.е. не подвергается действию входного сигнала.

3. Автомат без выхода. Множество Y состоит из одного элемента, т.е.

–автомат есть тройка 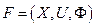и описывается соотношением

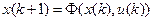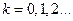, . (9)

4. Автомат с задержкой. Это автомат, у которого функция зависит только от состояния и не зависит от входа; соотношения (2), (3) имеют вид

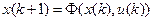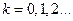, ; (10)

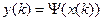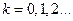, . (11)

5. Автомат Мура. Это автомат второго рода, в котором функция зависит только от состояния. Соотношения (4), (5) имеют вид

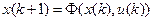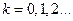, ; (12)

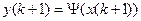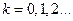. . (13)

Чтобы задать конечный -автомат, необходимо описать все элементы множества 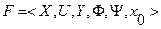, т.е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов. Причем среди множества состояний необходимо выделить состояние . Существуют несколько способов задания работы - автомата, но наиболее часто используются табличный, графический и матричный способы. Наиболее наглядным является табличный способ, основанный на использовании таблиц переходов и выходов.

Описание работы -автомата Мили с помощью таблиц переходов и выходов представлено таблицей 3.1, а описание работы -автомата Мура с помощью таблицы переходов – таблицей 3.2.

Таблица 3.1 F-автомат Мили

		…
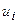
Переходы
	, )		…
			…
…	…	…	…	…
			…
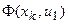
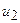
Выходы
			…
			…
…	…	…	…	…
			…

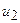
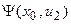
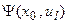
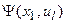
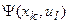
Таблица 3.2 F-автомата Мура

		…
		…
	(	(	…	(
			…
…	…	…	…	…
			…

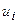
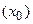
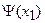
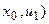
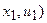
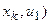
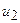
При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал 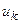вызывает переход из состояния в состояние , то на графе автомата дуга, соединяющая вершину с вершиной , помечается значением 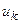. Для того, чтобы задать функцию выходов, дуги графа необходимо пометить соответствующими выходными сигналами.

Для автомата Мили эта разметка производится следующим образом. Если входной сигнал 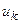действует на состояние , то формируется дуга, исходящая из состояния и помеченная 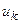; эту дугу дополнительно отмечают выходным сигналом y= .

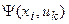Для автомата Мура, если входной сигнал 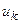, действуя на некоторое состояние автомата 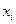, вызывает переход в состояние , то дугу, направленную от 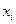к и помеченную 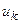, дополнительно помечают выходным сигналом y= .

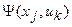При решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица C= 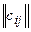, строки которой соответствуют исходным состояниям, а столбцы – состояниям перехода. Элемент = , стоящий на пересечении – ой строки и 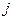– го столбца, в случае автомата Мили соответствует входному сигналу 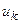, вызывающему переход из состояния в состояние , и выходному сигналу , определяемому состоянием 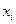. Для автомата Мура выходной сигнал определяется состоянием .

Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние.

Дата добавления: 2014-12-27