Процессы в системах массового обслуживания как непрерывные

марковские процессы ()

Рассмотрим некоторые модели СМО, для которых граф переходов связан с одной типичной схемой непрерывных марковских цепей – так называемой «схемой гибели и размножения».

Марковская непрерывная цепь называется «процессом гибели и размножения», если ее граф состояний имеет вид, представленный на рисунке 3.1. Здесь все состояния вытянуты в цепочку, в которой каждое из средних состояний связано с каждым из соседних состояний, а крайние состояния – только с одним соседним состоянием.

Рис. 3.1 Размеченный граф для «процесса гибели и размножения»

Схема гибели и размножения часто встречается в самых разнообразных практических задачах и, в частности, в задачах теории массового обслуживания. Обычно в таких задачах за состояние системы оказывается возможным принять количество заявок в системе.

Небольшое число связей между состояниями приводит к тому, что системы дифференциальных и алгебраических уравнений относительно вероятностей состояний упрощается. В [7] приведены соотношения для расчета финитных значений вероятностей для различных частных типов задач.

Прежде всего это одноканальные и многоканальные СМО с отказами, с ожиданием, с ограниченным временем ожидания.

Рассмотрим в качестве общего примера следующую СМО смешанного типа. Имеется n-канальная СМО с ожиданием, на которую поступает поток заявок с интенсивностью ; интенсивность обслуживания для одного канала 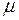; число мест в очереди m. Заявка, вставшая в очередь на обслуживание, после некоторого времени ожидания покидает систему необслуженной, т.е. на каждую заявку очереди как бы действует поток «уходов» с интенсивностью .

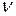Состояния будем определять количеством заявок в системе:

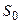– все каналы свободны, очереди нет,

– занят один канал, остальные свободны, очереди нет,

…..

– заняты k каналов, остальные свободны, очереди нет,

…..

– заняты все n каналов, очереди нет,

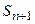– заняты все n каналов, одна заявка стоит в очереди,

…..

– заняты все n каналов, r заявок стоят в очереди,

…..

– заняты все n каналов, m заявок стоят в очереди.

Размеченный граф переходов представлен на рисунке 3.2.

Рис. 3.2 Размеченный граф для n-канальной СМО с m-местной очередью

Если длина очереди не ограничена по условию задачи каким-либо числом, схема должна быть неограниченно продолжена вправо, т.е. правая часть схемы изображена как на рисунке 3.3.

Рис. 3.3 Часть графа, в случае СМО с неограниченным числом мест в очереди

Как видно из графа (рис. 3.1), мы имеем схему гибели и размножения. Выражения для предельных вероятностей системы имеют вид:

;

…

…..

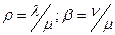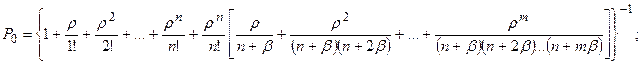
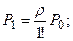
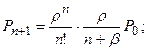
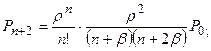
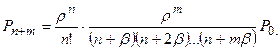
Если длина очереди не ограничена и заявка не уходит из очереди, то стационарный предельный режим существует только при (при 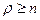соответствующая бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при t ).

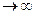Если заявки уходят из очереди, установившийся режим обслуживания при t 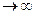достигается всегда, независимо от отношения 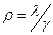, так как ряд в знаменателе формулы для сходится при любых положительных и .

В схему гибели и размножения вписываются также замкнутые системы.

В отличие от рассмотренной в предыдущем примере СМО, в этих системах поток заявок на обслуживание зависит от состояния системы. Типичным примером такой системы является система, включающая бригаду наладчиков и группу станков, которые она обслуживает. Пусть m-число рабочих и n-число станков (n>m). Каждый рабочий занят наладкой (или ремонтом) одного станка. Система имеет ряд состояний, которые могут быть пронумерованы числом неисправных станков:

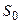– все станки исправны, все рабочие свободны, очереди нет,

– один станок неисправен, один рабочий занят его наладкой, очереди нет,

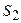– два станка неисправны, два рабочих заняты наладкой, очереди нет,

…..

– m станков неисправны, все рабочие заняты, очереди нет,

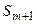– m+1 станок неисправен, все рабочие заняты, один станок ожидает

наладки,

…..

– все станки неисправны, все рабочие заняты, (n-m) станков ожидают

наладки,

– поток отказов для одного станка,

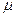– поток наладок для одного рабочего.

Размеченный граф переходов для этой системы имеет вид, представленный на рисунке 3.4

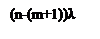
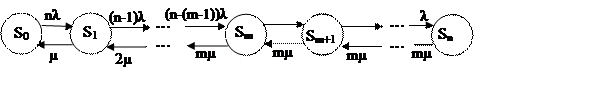
Рис. 3.4 Размеченный граф для системы обслуживания n-станков m-рабочими

Обозначив формулы для предельных вероятностей можно записать в виде:

…..

…..

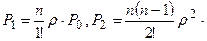
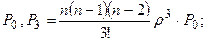
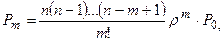
Наконец следует остановиться на СМО, имеющих циклический тип графа переходов. Марковский случайный процесс называют циклическим, если состояния связаны между собой в кольцо (цикл с односторонними переходами).

Во многих случаях приходится иметь дело с ветвящимся циклическим процессом, Если граф состояний в отдельных узлах образует разветвления. Примером такой системы может являться система обслуживания какой-либо технической установки. Установка может, например, находиться в следующих состояниях:

– исправна, нормально функционирует,

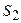– неисправна, остановлена, ведется поиск неисправности,

– неисправность незначительна, ведется мелкий ремонт,

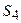– неисправность средней тяжести, ведется средний ремонт,

– неисправность значительна, ведется капитальный ремонт,

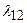– поток отказов установки,

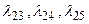– потоки событий обнаружения и классификации неисправностей соответственно типам ремонта,

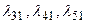– потоки восстановления соответственно типам ремонта.

Размеченный граф переходов представлен на рисунке 3.5

Рис. 3.5 Размеченный граф для циклического процесса

В соответствии с графом переходов (рис. 3.5) дифференциальные уравнения для вероятностей состояний i=1,2,…,5, имеют вид:

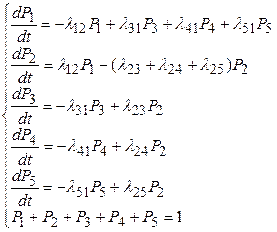Система 1

В качестве начальных условий для их решения можно, например, принять:

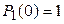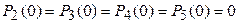; (или любое другое удовлетворяющее условию ).

Установившиеся или финитные значения вероятностей являются решением системы линейных алгебраических уравнений, полученных из системы 1, если положить 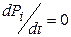, i=1,..5.

Дата добавления: 2014-12-27