Непрерывно-стохастическая модель. Системы массового обслуживания

Для описания такого рода систем используют типовые математические схемы, называемые системами массового обслуживания (англ. queueing system), которые иногда именуют Q-схемами.

Этому классу математических схем следует уделить особое внимание по двум соображениям. Во-первых, многие элементы и подсистемы различных сложных систем хорошо описываются как системы массового обслуживания. Поэтому модели типичных систем этого класса представляют непосредственный интерес. Кроме того, приемы моделирования, характерные для систем массового обслуживания, широко используются при построении моделей для сложных систем других типов и, прежде всего, моделей систем, включающих элементы более общего описания – агрегатов.

Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания для исследования процессов функционирования систем, которые по своей сути являются процессами обслуживания. Это процессы функционирования экономических, производственных, технических информационных систем. Характерным для таких систем является появление заявок (требований) на обслуживание в случайные моменты времени.

Рассмотрим некоторые понятия теории массового обслуживания, необходимые для построения и использования Q-схем.

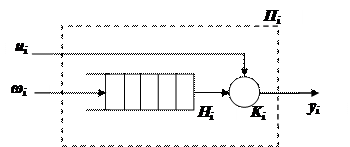
Рис. 3.6 Схема элементарного прибора обслуживания

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это отображено в схеме элементарного i-го прибора обслуживания 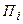(рис. 3.6), состоящего из накопителя заявок 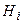, в котором может одновременно находиться 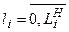заявок, где 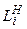– емкость i-го накопителя, и канала обслуживания заявок 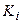. На каждый элемент прибора обслуживания 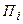поступают потокисобытий: в накопитель 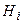– поток заявок 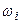, а на канал 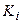– поток обслуживаний 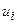.Заявки, обслуженные каналом 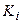, и заявки, покинувшие прибор 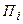по различным причинам необслуженными (например, из-за переполнения накопителя), образуют выходной поток .

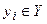Моделирование систем в классе математических схем теории массового обслуживания складывается, главным образом, из моделирования потоков заявок и моделирования совокупности обслуживающих каналов. Для этого нужно уметь задать характеристики потоков заявок и потоков обслуживания заявок по отдельным каналам.

Для этих потоков важными характеристиками являются:

· однородность (неоднородность);

· стационарность (нестационарность);

· ординарность;

· рекуррентность;

· наличие последействия (без последействия, с ограниченным последействием).

.

Поток заявок 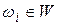, т.е. интервалы времени между моментами появления заявок (вызывающие моменты) на входе в 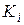, есть подмножество неуправляемых переменных, а поток обслуживания 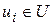, т.е. интервалы между началом и окончанием обслуживания заявки, есть подмножество управляемых переменных.

Процесс функционирования прибора 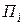можно представить как процесс изменения множества X состояний его элементов во времени 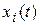. Переход в новое состояние для 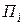означает изменение количества заявок, которые в нем находятся (в канале 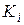и в накопителе 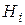). Таким образом, вектор состояний для 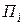имеет вид 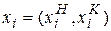, где 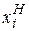- состояние накопителя 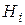( 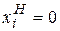– накопитель пуст, 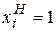– в накопителе имеется одна заявка, …, 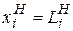– накопитель полностью заполнен); 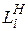- емкость накопителя 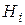, измеряемая числом заявок, которые в нем могут поместиться, 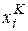- состояние канала 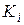( 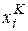=0 – канал свободен, 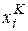=1 – канал занят).

На практике в более сложных случаях для формализации обычно используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов 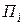. Если каналы 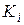различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы 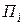и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой.

Различают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует. В замкнутых схемах имеются обратные связи, по которым заявки двигаются в направлении обратном движению вход-выход.

Собственные (внутренние) параметры Q-схемы:

· количество фаз ;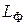

· количество каналов в каждой фазе , ;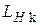

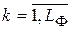· емкость i-го накопителя .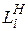

Для систем массового обслуживания применяется следующая терминология:

· системы с потерями (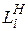 =0, т.е. накопитель в приборе 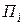отсутствует, а имеется только канал обслуживания );

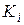· системы с ожиданием (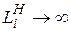, т.е. накопитель 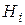имеет бесконечную емкость, и очередь заявок не ограничивается);

· системы смешанного типа (с ограниченной емкостью накопителя ).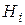

Всю совокупность собственных параметров Q-схемы обозначим как подмножество H.

Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, описывающие набор правил поведения заявок в различных ситуациях. В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе 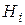и алгоритмы обслуживания заявок каналом 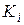каждого элементарного обслуживающего прибора 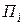Q-схемы. Неоднородность заявок учитывается с помощью введения классов приоритетов.

В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы. Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций. Исходя из правил выбора заявок из накопителя 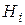на обслуживание каналом 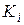, можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель 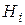, ожидает окончания обслуживания предшествующей заявки каналом 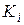и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель 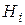, прерывает обслуживание каналом 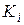заявки с более низким приоритетом и сама занимает канал (при этом вытесненная из канала заявка может либо покинуть систему, либо может быть снова поставлена на какое-то место в накоптель).

Приведем, следуя [8], ставшую общепринятой при описании простых систем с очередями нотацию Кендалла – Башарина. В этой нотации система массового обслуживания кодируется пятью позициями: A/B/m/K/N, где A обозначает распределение интервалов во входном потоке, B – распределение времени обслуживания, m – количество каналов обслуживания, K – емкость системы, то есть максимально возможное число заявок в ней, N – количество источников в нагрузке. Поля A и B могут принимать значения: M – экспоненциальное распределение (буква M символизирует марковское свойство или свойство отсутствия последействия): 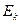– 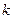-фазное распределение Эрланга; 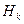– 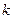-фазное гиперэкспоненциальное распределение; – детерминированная величина; – произвольное распределение; 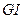– произвольное распределение с независимыми интервалами.

Принят также следующий перечень для наиболее распространенных дисциплин обслуживания:

· FCFS – (First come – First Served) – обслуживание в порядке поступления в очередь (по умолчанию применяется именно эта дисциплина);

· LCFS – (Last come – First Served) – из очереди выбирается заявка, пришедшая последней;

· SIRO – (Service in Random Order) – заявка выбирается из очереди случайным образом;

· RR – (Round Robbin) – применяется дисциплина FCFS, обслуживание заявки прерывается, если оно не завершено в течение выделенного отрезка времени, и заявка возвращается в очередь (эта процедура может повторяться, пока обслуживание заявки не завершится);

· SIF – (Shortest Job First) – первой обслуживается заявка наименьшей длины; применение этой дисциплины минимизирует среднее время ожидания и осуществимо, если время обслуживания заявки может быть оценено при постановке её в очередь;

· PS – (Processor Sharing) – предельный случай дисциплины 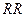, когда размер интервала обслуживания стремится к нулю; все заявки обслуживаются одновременно, очередь как таковая отсутствует, ресурс обслуживания делится поровну между всеми заявками;

· IS – (Infinite Server) – число каналов обслуживания настолько велико, что очередь никогда не образуется;

· Static Priorities – выбор заявки зависит от приоритетов, которые назначаются заявкам; внутри класса заявок с одинаковым приоритетом применяется дисциплина FCFS;

· Dynamic Priorities – выбор заявки зависит от динамических приоритетов, которые меняются с течением времени;

· Preemption – прерывание обслуживания заявки, если поступила заявка с более высоким приоритетом, и немедленный захват канала.

Дисциплины Static Priorities и Dynamic Priorities являются относительными приоритетами, а Preemption – абсолютным приоритетом. В случае абсолютных приоритетов возможны три варианта дальнейших действий для прерванной заявки:

· обслуживание возобновляется с места прерывания;

· обслуживание начинается сначала, длина заявки сохраняется;

· обслуживание начинается сначала, длина заявки разыгрывается заново.

Алгоритмы обслуживания описывают также набор правил, по которым заявки могут покидать систему, а каналы могут быть блокированы. Это, например, правила переполнения накопителя и ухода заявок из очереди в связи с истечением времени ожидания обслуживания. Весь набор правил поведения заявок в Q-схеме можно представить в виде алгоритма A. Таким образом Q-схема полностью задается шестеркой Q =(W,U,H,X,R,A);

Дата добавления: 2014-12-27