Обобщенные модели

Наиболее известный в России подход к формальному описанию процессов функционирования сложных систем принадлежит Н.П. Бусленко [2]. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т.е. он является обобщенным и базируется на понятии агрегативной системы (англ. aggregate system), так называемой А-схемы.

Многое говорит за справедливость утверждения – моделирующие системы должны иметь в своей основе единую формальную математическую схему, т.е. А-схему. Такая схема должна одновременно выполнять несколько функций:

· являться адекватным математическим описанием объекта моделирования;

· служить основой для построения алгоритмов и программ при машинной реализации модели;

· позволять в упрощенном варианте (для частных случаев) проводить аналитические исследования.

В качестве элементов А-схемы выступают агрегаты, а связь между агрегатами (внутри системы) и с внешней средой осуществляется с помощью оператора сопряжения R. Вообще говоря, и сам агрегат может рассматриваться как А-схема, т.е. может разбиваться на элементы (агрегаты) следующего уровня.

Любой агрегат характеризуется следующими множествами:

· моментов времен T;

· входных сигналов U;

· выходных сигналов Y;

· состояний X в каждый момент времени t.

Состояние агрегата в момент времени 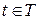обозначается как 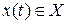, а входные и выходные сигналы, как 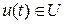и 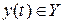соответственно.

Будем полагать, что переход агрегата из состояния 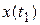в состояние происходит за малый интервал времени, т.е. имеет место скачок . Переходы агрегата из состояния в состояние определяются собственными (внутренними) параметрами самого агрегата и входными сигналами .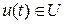

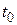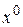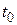В начальный момент времени состояния x имеют значения, равные , т.е. , задаваемые законом распределения процесса в момент времени , а именно 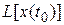. Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала 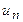описывается случайным оператором V. Тогда в момент 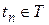поступления в агрегат входного сигнала 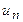можно определить состояние .

Обозначим полуинтервал времени как , а полуинтервал как . Если интервал времени не содержит ни одного момента поступления сигналов, то для состояние агрегата определяется случайным оператором Z в соответствии с соотношением .

Совокупность случайных операторов V и Z можно рассматривать как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний в моменты поступления входных сигналов u (оператор V) и изменений состояний между этими моментам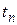и и 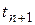(оператор Z). При этом допускается как непрерывное, так и дискретное изменение состояний в моменты времени, не являющиеся моментами поступления входных сигналов u. Принято в дальнейшем моменты скачков называть особыми моментами времени , а состояния - особыми состояниями А-схемы. Для описания скачков состояний в особые моменты времени используют случайный оператор W, представляющий собой частный случай оператора Z, т.е. .

Во множестве состояний X выделяется такое подмножество , что если достигает , то это состояние является моментом выдачи выходного сигнала, определяемого оператором выходов .

Таким образом, под агрегатом понимается любой объект, определяемый упорядоченной совокупностью рассмотренных множеств T, U, Y, X, , H ислучайных операторов V, Z, W, G.

Последовательность входных сигналов, расположенных в порядке их поступления в А-схему, называется входным сообщением или u -сообщением. Последовательность выходных сигналов, упорядоченная относительно времени выдачи, называется выходным сообщением или y -сообщением.

Конструкция из отдельных агрегатов , , 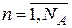составляющая модель сложной системы, называется агрегативной системой или А-схемой. Для ее описания необходимо иметь описание как отдельных агрегатов, так и связей между ними.

Вообще говоря, любая система, при моделировании которой важно рассматривать как возможность непрерывного изменения ее состояния, так и изменение ее состояния скачком, является агрегатом или агрегативной системой.

В этом отношении система массового обслуживания при моделировании ее по «принципу » (изменение времени с постоянным шагом) может рассматриваться как агрегативная система. В этом случае «непрерывными» переменными состояния являются времена, оставшиеся до окончания обслуживания, до момента поступления заявки, до момента отказа и т.д. В качестве дискретно изменяющихся переменных состояния могут рассматриваться число заявок в накопителях, состояния каналов и т.д. Входные и выходные сигналы – это собственно информация о поступлении в систему или выходе из системы заявок. Соответственно это описывается всеми приведенными выше операторами.

К агрегативным системам следует также отнести и некоторые, вообще говоря, непрерывные системы, параметры которых могут изменяться скачком в зависимости от положения изображающей точки в фазовом пространстве или от входного сигнала. Сюда можно отнести системы с переменной структурой, многорежимные системы управления, системы, функционирующие в условиях различного рода отказов и т.д. В частности, сюда можно отнести, исходя из этих же соображений, и оптимальные по быстродействию системы управления.

Дата добавления: 2014-12-27