Ортогональные центральные композиционные планы

В планах Бокса к ядру, построенному на основе ПФЭ или ДФЭ, добавляется одна точка в центре плана с координатами (0, 0,..., 0) и 2 k "звездных" точек с координатами

(± g, 0,..., 0),..., (0, 0,..., ± g).

Построенный таким образом план будет ЦКП второго порядка. Общее точек плана при использовании композиционного планирования составит N = N ₀+2 k+ 1, где N ₀ – количество точек ядра плана. В табл. 5.1 и 5.2 содержится описание соответствующих матриц планирования для ЦКП при k =2. Количество опытов для данного плана N =2²+2·2+1=9. Аналогично строятся ЦКП для произвольного числа факторов, при этом каждый фактор варьируется на пяти уровнях: – g; – 1; 0; 1; g.

Таблица 5.1

Ядро плана
x 1	x 2
+	+
–	+
+	–
–	–

Таблица 5.2

Дополнительные точки
x 1	x 2
g
-g
	g
	-g

В матрице плана второго порядка не у всех столбцов соблюдается условие симметрии и не все пары столбцов ортогональны. Например, рассмотрим ЦКП второго порядка для трех переменных, табл. 5.3.

Таблица 5.3

План	x 0	x 1	x 2	x 3	x 1 x 2	x 1 x 3	x 2 x 3	x 1^2	x 2^2	x 3^2
ПФЭ	+	–	–	–	+	+	+	+	+	+
	+	+	–	–	–	–	+	+	+	+
	+	–	+	–	–	+	–	+	+	+
	+	+	+	–	+	–	–	+	+	+
	+	–	–	+	+	–	–	+	+	+
	+	+	–	+	–	+	–	+	+	+
	+	–	+	+	–	–	+	+	+	+
	+	+	+	+	+	+	+	+	+	+
Звездный	+	–g						g^2
план	+	g						g^2
	+		–g						g^2
	+		g						g^2
	+			–g						g^2
	+			g						g^2
Центр	+

Суммы

так как

для всех строк плана.

Для устранения асимметрии и нарушений ортогональности ЦКП Бокса необходимо провести преобразование квадратичных параметров и специальным образом выбрать величину плеча g.

Чтобы добиться соблюдения свойства симметричности следует перейти от x_i ² к центрированным величинам x_i ^* = x_i ² – x ² _{i ср} (сумма центрированных величин равна нулю). Среднее значение x ² _{i ср}, как видно из табл. 5.3, для всех x_i ² одинаково и равно

c = (N 0+2g^2)/ N.	(5.3)

Тогда исходную квадратичную модель (5.1) можно преобразовать

y^' =b₀ + b₁ x ₁+ … + b₁ x_k + b₁₂ x ₁ x ₂ + … + b _{k –1, k} x_{k– 1} x_k +

+b₁₁(x ₁² – x ²_{1 ср} + x ²_{1 ср}) + … + b _kk (x_k ² – x ² _{k ср} + x ² _{k ср}) =

= d ₀ + b₁ x ₁+ … + b₁ x_k + b₁₂ x ₁ x ₂ + … + b _{k –1, k} x_{k– 1} x_k +b₁₁ x ₁^* + … + b _kkx_k ^*,

где d ₀ = b₀ + b₁₁ x ²_{1 ср} + … + b _{k –1, k} x ² _{k ср} = b₀ + c (b₁₁ + … + b _{k –1, k}).

Исходная и преобразованная модели эквивалентны, в них все коэффициенты, за исключением нулевого, совпадают.

После преобразования получим матрицу планирования, табл. 5.4.

Таблица 5.4

План	x0	x1	x2	x3	x1 x 2	x1 x 3	x2 x 3	x1^*	x2^*	x3^*
ПФЭ	+	–	–	–	+	+	+	1–с	1–с	1–с
	+	+	–	–	–	–	+	1–с	1–с	1–с
	+	–	+	–	–	+	–	1–с	1–с	1–с
	+	+	+	–	+	–	–	1–с	1–с	1–с
	+	–	–	+	+	–	–	1–с	1–с	1–с
	+	+	–	+	–	+	–	1–с	1–с	1–с
	+	–	+	+	–	–	+	1–с	1–с	1–с
	+	+	+	+	+	+	+	1–с	1–с	1–с
Звездный	+	–g						g^2–с	–с	–с
план	+	g						g^2–с	–с	–с
	+		–g					–с	g^2–с	–с
	+		g					–с	g^2–с	–с
	+			–g				–с	–с	g^2–с
	+			g				–с	–с	g^2–с
Центр плана	+							–с	–с	–с

Нетрудно заметить, что в этой таблице суммы элементов по всем столбцам, за исключением столбца x ₀, равны нулю, т.е. в преобразованной таблице соблюдается свойство симметричности. Но столбцы квадратичных членов не являются ортогональными при произвольных значениях g

Ортогонализация столбцов, т. е. приравнивание

к нулю, достигается специальным выбором величины g. Это значение величины g находится из уравнения

или

N ₀ – 2 сN ₀ + N ₀ с ² – 4 c g² +4 c ² + 2 kс ² – 4 c ² + c ² =

N ₀ – 2(N ₀ +2g²) с + c ² (N ₀ + 2 k +1)= N ₀ – 2 с ² N + c ² N = 0.

Следовательно, с ² N = N ₀. Тогда с = (N ₀ / N)^1/2. Подставим найденное значение величины с в уравнение (5.2)

(N ₀ / N)^{1/ 2} = (N ₀ + 2g²)/ N.

Решив уравнение, найдем величину g, которая придает матрице планирования (в том числе табл. 5.4) свойство ортогональности

g = {[(N N 0)^1/2– N 0]/2}^1/ 2.

(5.3)

Значения g, обеспечивающие ортогональность, например, для ядер 2², 2³, 2⁴, 2^5–1, составляют соответственно 1; 1,215; 1,414; 1,547.

Оценки коэффициентов регрессии определяются по модифицированной матрице независимых переменных, табл. 5.4:

В приведенной формуле m равно числу сочетаний из k +2 по два и обозначает общее количество оцениваемых коэффициентов полинома, за исключением нулевого.

Оценка коэффициента

,

тогда

.

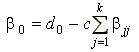Оценки дисперсии коэффициентов

;

,

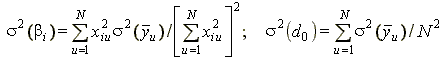где 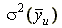– оценка дисперсии среднего значения функции отклика в u -й точке плана.

Оценка дисперсии функции отклика

.

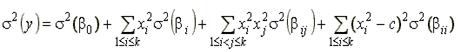Оценки дисперсии коэффициентов являются различными, так как вычисляются по разным совокупностям точек плана. Оценка дисперсии функции отклика зависит не только от расстояния до заданной точки от центра, но и от ее положения в пространстве, т. е. ортогональный план второго порядка не являются ротатабельным.

Проверка однородности дисперсии воспроизводимости, адекватности модели, значимости коэффициентов полинома в случае применения ортогональных ЦКП второго порядка осуществляется по рассмотренной выше схеме.

Дата добавления: 2014-12-27