Дифференцирование булевых функций

Полнота

Выделяются следующие классы булевых функций:

1. Класс функций, сохраняющих 0:

T ₀ = { f | f (0, …,0) = 0}.

2. Класс функций, сохраняющих 1:

T ₁ = { f | f (1, …,1) = 1}.

3. Класс самодвойственных функций:

T _* = { f | f = f^* }.

4. Класс монотонных функций:

T _< = { f | a £ b Þ f (a) £ f (b)},

где a = (а ₁ ,...,а_n), b = (b ₁, …, b_n), а_i, b_i Î Е₂, a < b = " i a_i £ b_i.

5. Класс линейных функций:

T_L = { f | f = c ₀Å c ₁ x ₁Å … Å c_nx_n }.

где + обозначает сложение по модулю 2, а знак конъюнкции опущен.

Множество функций F образует полную систему, если любая функция реализуема в виде формулы над F.

ТЕОРЕМА (Пост) Система булевых функций F полна тогда и только тогда, ко­гда она содержит хотя бы одну функцию, не сохраняющую нуль, хотя бы одну функцию, не сохраняющую единицу, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию и хотя бы одну нелинейную функцию.

Пример

Системы {Ú, Ø}, {Ù, Ø} являются полными.

Производная первого порядка от булевой функции f по переменной x_i есть сумма по модулю 2 соответствующих оста­точных функций:

где – единичная остаточная функ­ция;

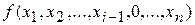– нулевая остаточная функция

Производная первого порядка от булевой функции опре­деляет условия, при которых эта функция изменяет значение при переключении переменной x_i (при переменной значения x_i на противоположное).

Пример

Вычислим производную от булевой функции .

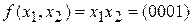. Согласно определению

.

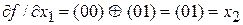Смешанной производной от булевой функции f по переменным ( называется выраже­ние вида

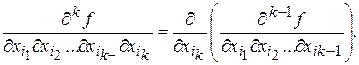
Смешанную производную k -го порядка вычисляют, определяя производную первого порядка k раз фиксацией переменных 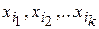(порядок фиксации переменных не имеет значения); количество упорядочиваний равно k!

Производная k-го порядка от булевой функции 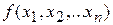по переменным 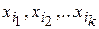опре­деляет условия, при которых эта функция изменяет значение при одновременном изменении значений переменных .

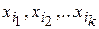Дата добавления: 2014-12-27