Элементы графов

Подграфы

Граф G' (V’, Е ')называется подграфом графа G (V, E)(обозначается G' Ì G), если V’ Ì V и/или Е' Ì Е.

Если V’ = V, то G' называется остовным подграфом G.

Если V’ Ì V & E' Ì E & (V‘ ¹ V V Е' ¹ Е), то граф G’ называется собственным подграфом графа G.

Подграф G' (V',E')называется правильным подграфом графа G (V,E), если G' содержит все возможные ребра G:

" u, v Î V’ (u,v) Î E => (u, v) Î Е'.

Правильный подграф G' (V’, Е') графа G (V, e) определяется подмножеством вер­шин V’.

Валентность

Количество ребер, инцидентных вершине v, называется степенью (или валент­ностью) вершины v и обозначается d (v):

" u, v Î V 0 £ d (v)£ p– 1, d(v) = |Г(v)|.

Обозначим минимальную степень вершины графа G через d(G), а максималь­ную — через D(G):

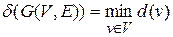
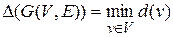
Если степени всех вершин равны k, то граф называется регулярным степени k:

d (G) = D(G) = k.

Маршруты, цепи, циклы

Маршрутом в графе называется чередующаяся последовательность вершин и ребер, в которой любые два соседних элемента инцидентны.

Если v₀ = v_k, то маршрут замкнут, иначе открыт.

Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью. В цепи v₀, e₁,...,e_k, v_k вершины v₀ и v_k называются концами цепи. Говорят, что цепь с концами и и v соединяет вершины и и v. Цепь, соединяющая вершины и и v, обозначается (u,v). Очевидно, что если есть цепь, соединяющая вершины и и v, то есть и простая цепь, соединяющая эти вершины.

Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z (G). Граф без циклов называется ациклическим.

Для орграфов цепь называется путем, а цикл — контуром.

Расстояние между вершинами

Длиной маршрута называется количество ребер в нем (с повторениями). Если маршрут М = v₀, e₁, v₁, e₂, v₂, …,e_kv_k, то длина М равна k (обозначается | М| = k).

Расстоянием между вершинами и и v (обозначается d (u,v))называется длина кратчайшей цепи (u, v), а сама кратчайшая цепь называется геодезической.

Диаметром графа G (обозначается D (G))называется длина длиннейшей геоде­зической.

Множество вершин, находящихся на одинаковом расстоянии п от вершины v (обозначение D (v,n)), называется ярусом:

D (v, n) = { u 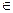V | d (v, u)= n }.

Связность

Говорят, что две вершины в графе связаны, если существует соединяющая их (простая) цепь. Граф, в котором все вершины связаны, называется связным.

Отношение связанности вершин является эквивалентностью. Классы эквива­лентности по отношению связанности называются компонентами связности гра­фа. Число компонент связности графа G обозначается k (G). Граф G является связным тогда и только тогда, когда k (G)= 1. Если k (G) > 1, то G — несвязный граф. Граф, состоящий только из изолированных вершин (в котором k (G)= p (G)и r (G) = 0), называется вполне несвязным.

6.3. Представление графов

Матрица смежности

Представление графа с помощью квадратной булевской матрицы размером p ´ p, отражающей смежность вершин, называется матрицей смежности, где

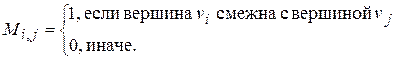
Матрица инциденций

Представление графа с помощью матрицы Н размером p ´ q, отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа

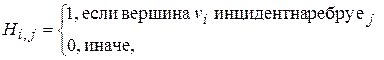
а для ориентированного графа

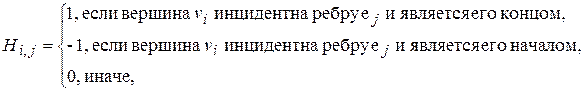
Граф можно задать также посредством списков:

1) Списком пар вершин, соединенных ребрами (или дугами).

2) Списком списков для каждой вершины множества смежных с ней вершин.

Пример

Пусть даны два графа. Неориентированный граф показан на рисунке 6.2, а, ориентированный – на рисунке 6.2, б. Построим матрицы смежности, матрицы инцидентности, списки пар вершин и списки списков для данных графов.

Матрица смежности неориентированного графа:

.

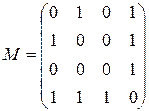Матрица смежности ориентированного графа:

.

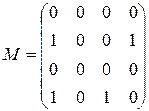Матрица инцидентности неориентированного графа:

.

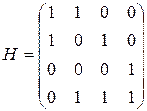Матрица инцидентности ориентированного графа:

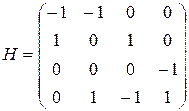
Список пар вершин неориентированного графа: ({1,2}, {1,4}, {2,4}, {3,4}).

Список пар вершин ориентированного графа: ((1,2), (1,4), (4,2), (3,4)).

Список списков неориентированного графа: ((2,4), (1,4), (4), (1,2,3)).

Список списков ориентированного графа: ((2,4), Æ, (4), (2)).

Дата добавления: 2014-12-27