
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальные формы
|
|
|
|
Формулы
Пусть F = { f 1, …, fm } – множество булевых функций. Формулой над F называется выражение вида f (t 1, …, tn), где t 1, …, tn либо переменные, либо формулы. Множество F называется базисом, функция f называется главной (внешней) операцией формулы.
Обычно для элементарных булевых функций используется инфиксная форма записи, устанавливается приоритет (Ø, &, Å, 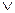 , ®, «) и лишние скобки опускаются.
, ®, «) и лишние скобки опускаются.
Одна функция может иметь множество реализаций (над данным базисом). Формулы, реализующие одну и ту же функцию, называются равносильными. Отношение равносильности формул является эквивалентностью. Имеют место следующие равносильности:
1. 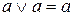 ,
, 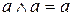 ;
;
2. 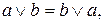
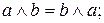
3. 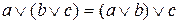 ,
, 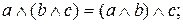
4. 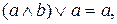
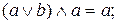
5. 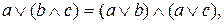
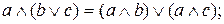
6. 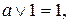
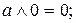
7. 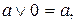
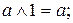
8. 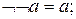
9. 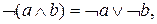
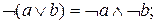
10. 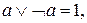
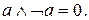
Совершенная дизъюнктивная нормальная форма
В данном разделе на примере булевых функций обсуждается важное понятие «нормальной формы», то есть синтаксически однозначного способа записи формулы, реализующей заданную функцию.
ТЕОРЕМА (О разложении булевой функции по переменным)
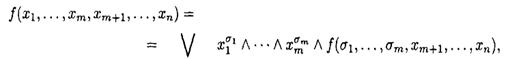
(s1, …,sm)
где дизъюнкция берется по всем возможным наборам(s 1, …,sm).
Представление булевой функции f (x 1 ,..., xn) в виде
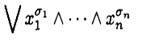
называется совершенной дизъюнктивной нормальной формой (СДНФ).
Пример
x Å y = x Ø y Ú Ø xy
Минимизация булевых функций
Минимизацией булевых функций называется их представление в виде СДНФ, которая содержит наименьшее число переменных и их отрицаний.
Формула, представленная в виде СДНФ, упрощается многократным применением операций склеивания
ab Ú a Ø b = a
и операций поглощения
a Ú ab = a, a Ú Ø ab = a Ú b.
Если дальнейшие преобразования невозможны, то говорят, что имеет место тупиковая форма. Таких форм может быть несколько.
Пример
Ø xy Ø z Ú Ø xyz = Ø xy
Графический метод минимизации булевых функций
Рассматриваемый графический метод использует диаграммы Вейча, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы также считаются соседними.
Клетки, в которых функция принимает значение 1, заполняются единицами. Соседние клетки, содержащие единицы, объединяются в области. Каждая единица может находиться сразу в нескольких областях, но число областей должно быть минимальным.
Таким образом, каждая полученная область будет соответствовать конъюнкции переменных или их отрицаний (это видно по диаграмме), а сама минимизированная СДНФ будет представлять собой дизъюнкцию этих конъюнкций.
На рисунке 5.1 представлены диаграммы Вейча для функций двух, 3-х, и 4-х переменных. Числа в клетках соответствуют бинарному коду набора значений переменных функции.
| x 1 | Ø x 1 | |
| x 2 | ||
| Ø x 2 |
| x 1 | Ø x 1 | |||
| X 3 | ||||
| Ø x 3 | ||||
| Ø x 2 | x 2 | Ø x 2 |
| x 1 | Ø x 1 | ||||
| x 3 | Ø x 4 | ||||
| x 4 | |||||
| Ø x 3 | |||||
| Ø x 4 | |||||
| Ø x 2 | x 2 | Ø x 2 |
Рис. 5.4. Диаграммы Вейча для функций двух, 3-х, и 4-х переменных
Пример
f (x 1, x 2) = x 1 ® x 2 = (1101) – значения функции в таблице истинности.
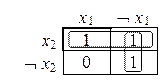
Видно, что первая область соответствует переменной x 2, а вторая Ø x 1.
Следовательно, f (x 1, x 2) = x 2 Ú Ø x 1.
Пример
f (x 1, x 2, x 3) = (1001 1100)
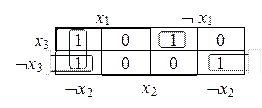
f (x 1, x 2, x 3) = x 1Ø x 2 Ú Ø x 1 x 2 x 3 Ú Ø x 2Ø x 3.
Пример
f (x 1, x 2, x 3, x 4) = (1011 0110 0111 1111)
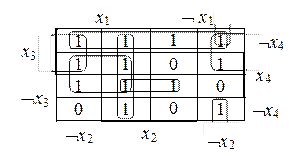
f (x 1, x 2, x 3, x 4) = Ø x 2 x 3Ø x 4 Ú x 3Ø x 4 Ú x 1 x 2 Ú Ø x 1Ø x 2Ø x 4 Ú x 1 x 4 Ú x 2Ø x 3 x 4.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!