
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебры с одной операцией
|
|
|
|
Морфизмы
Гомоморфизм
Алгебры с различными типами имеют различное строение.
Пусть A = (A; j 1 ,..., jm)и B = (В; 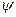 1, …,
1, …, 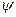 m) — две алгебры одинакового типа. Если существует функция f: А
m) — две алгебры одинакового типа. Если существует функция f: А  В, такая что
В, такая что
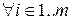 f (φ i(a 1,…, a n))= ψ i(f (a 1),…, f (a n)),
f (φ i(a 1,…, a n))= ψ i(f (a 1),…, f (a n)),
то говорят, что f — гомоморфизм из A в B.
Пример
Пусть A = (N; +), B = (N10; +10), где N10 = {0,1,2,3,4,5,6,7,8,9}, а +10 -сложение по модулю 10. Тогда f = a mod 10 — гомоморфизм из A в B.
Изоморфизм
Пусть A = (A; j 1, …, jm)и B = (В; 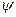 1 , …,
1 , …, 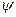 m) — две алгебры одного типа, и f: А ® В — изоморфизм.
m) — две алгебры одного типа, и f: А ® В — изоморфизм.
Пример
1. Пусть А = (N; +), B = {{ n | п = 2k, k Î N}; +) - четные числа. Тогда А изоморфна B по +.
2. А = (2 м; 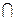 ,
, 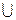 , Ø), B = (2 м;
, Ø), B = (2 м; 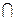 ,
, 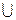 , Ø), f (X) = Ø X.
, Ø), f (X) = Ø X.
3. А = (R+; ×), B = (R; +).
ТЕОРЕМА Если f: А ® В — изоморфизм, то f- -1: А ® В тоже изоморфизм.
Полугруппы
Полугруппа — это алгебра с одной ассоциативной бинарной операцией:
а 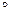 (b
(b 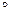 с) = (a
с) = (a 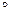 b)
b) 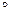 с.
с.
Пример
1. Множество слов А+ в алфавите А образует полугруппу относительно операции конкатенации.
2. Всякое множество функций, замкнутое относительно суперпозиции, является полугруппой.
Если в полугруппе существует система образующих, состоящая из одного элемента, то такая полугруппа называется циклической.
Пример
(N; +} является циклической полугруппой.
Моноиды
Моноид — это полугруппа с единицей:
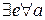
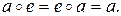
Пример
Множество слов А* в алфавите А вместе с пустым словом Lобразует моноид.
Группы
Группа — это моноид, в котором
" a $ а -1 а  a -1 = а -1
a -1 = а -1  a = е.
a = е.
Элемент а -1называется обратным.
Пример
1. Множество невырожденных квадратных матриц порядка n образует группу относительно операции умножения матриц. Единицей группы является единичная матрица. Обратным элементом является обратная матрица.
2. Множество подстановок на множестве М, то есть множество взаимно однозначных функций f: М ® М является группой относительно операции суперпозиции. Единицей группы является тождественная функция, а обратным элементом — обратная функция.
Коммутативная группа, то есть группа, в которой
а 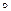 b = b
b = b 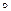 a,
a,
называется абелевой. В абелевых группах приняты следующие обозначения: групповая операция обозначается + или Å, обратный элемент к а обозначается -а, единица группы обозначается 0 и называется нулем.
Пример
(Z; +) — множество целых чисел образует абелеву группу относительно сложения. Нулем группы является число 0. Обратным элементом является число с противоположным знаком: х -1 := -х.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1388; Нарушение авторских прав?; Мы поможем в написании вашей работы!