Операции и алгебры

Упражнения

1. Определить , .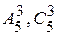

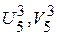2. Получить всевозможные комбинации перестановок множества { a, b, c }.

3. Получить всевозможные размещения и сочетания двух элементов множества { a, b, c }.

4. В мешке два красных, три синих и один белый шар. Сколькими способами можно вынуть цветной шар.

5. В одном мешке два красных, три синих и один белый шар, в другом три красных, пять синих и один черный шар. Сколькими способами можно вынуть два синих шара из двух мешков.

6. Доказать, что А (т, п) = А (т - 1, п) + пА (т - 1, п - 1).

7. Доказать, что mC (т - 1, п - 1) = пС (т, п).

Глава 4. Алгебраические структуры

Алгебраические структуры

Всюду определенная (тотальная) функция j: М^п ® М называется п-арной (п-местной) операцией на М.

Если операция j — бинарная (то есть j: М ´ М ® M), то будем писать aj b вместо j (a, b) или а b, где — знак операции.

Множество М вместе с набором операций å = { j ₁,..., j _m}, j _i: М^m ® М, где n_i — арность операции j_i, называется алгебраической структурой, универсальной алгеброй или просто алгеброй. Множество М называется основным (несущим)множеством, или основой (носителем);вектор арностей (n ₁,..., n_m)называется типом; множество операций å называется сигнатурой. Запись: (М;å) или (М; j₁,..., j _m).

Если в качестве j_i допускаются не только функции, но и отношения, то множе­ство М вместе с набором операций и отношений называется моделью.

В приложениях обычно используется следующее обобщение понятия алгебры. Пусть М = { M ₁,..., М_n } — множество основ, å = { j _i, …, j _m} – сигнатура, причем j_i : M_i1 ´ … ´ M_in. ® M_j. Тогда (M; å) называется многоосновной ал­геброй. Другими словами, многоосновная алгебра имеет несколько носителей, а каждая операция сигнатуры действует из прямого произведения некоторых но­сителей в некоторый носитель.

Замыкания и подалгебры

Подмножество X Ì М называется замкнутым относительно операции j, если

" x ₁ , …, x_n Î C j (x ₁ , …, x_n) Î X.

Если X замкнуто относительно всех j Î å,то(X; å _X) называется подалгеброй (M;å _X), где å _X = .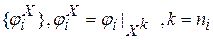

Пример

1. Алгебра { R; +, *} — поле действительных чисел. Тип — (2,2). Все конечные подмножества, кроме {0}, не замкнуты относительно обеих операций. Поле рациональных чисел (Q; +, *) образует подалгебру.

2. Алгебра (2 ^M; 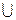, , 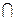^—) — алгебра подмножеств над множеством M. Тип — (2,2,1).При этом (2 ^M; 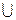, , 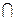^—) для любого подмножества X множества М обра­зует подалгебру.

3. Алгебра ({ f | f: R ® R }; 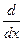), где 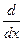— операция дифференцирования. Мно­жество элементарных функций образует подалгебру.

Свойства операций

Некоторые часто встречающиеся свойства операций имеют специальные назва­ния. Пусть задана алгебра (M; ∑) и a,b,c Тогда:

1. Ассоциативность: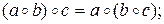

2. Коммутативность: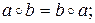

3. Дистрибутивность слева: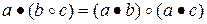

4. Дистрибутивность справа: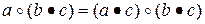

5. Поглощение: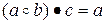

6. Идемпотентность:

Пример

1. Ассоциативные операции: сложение и умножение чисел, объединение и пере­сечение множеств, композиция отношений. Неассоциативные операции: воз­ведение чисел в степень, вычитание множеств.

2. Коммутативные операции: сложение и умножение чисел, объединение и пе­ресечение множеств. Некоммутативные операции: умножение матриц, компо­зиция отношений.

3. Дистрибутивные операции: умножение относительно сложения чисел. Недис­трибутивные операции: возведение в степень дистрибутивно относительно умножения справа, но не слева:

((ab) ^c = a^cb^c, a^bc ¹ а^bа^с).

4. Пересечение поглощает объединение, объединение поглощает пересечение. Сложение и умножение не поглощают друг друга.

5. Идемпотентные операции: наибольший общий делитель натуральных чисел, объединение и пересечение множеств. Неидемпотентные операции: сложение и умножение чисел.

Дата добавления: 2014-12-27