Функции. Понятие «функции» является одним из основополагающих в математике

Понятие «функции» является одним из основополагающих в математике. В дан­ном случае подразумеваются прежде всего функции, отображающие одно конеч­ное множество объектов в другое конечное множество.

Определения

Пусть f — отношение из А в В, такое что

" a (a, b) 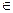f & (a, с) Î f 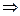b = с.

Такое свойство отношения называется однозначностью, или функциональностью, а само отношение называется функцией (или отображением)из А в В и обозначается следующим образом:

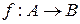или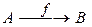

Если f: А ® В, то обычно используется префиксная форма записи:

b = f (a) Û (a, b) Î f

Если b = f (а), то а называют аргументом, а b — значением функции.

Инъекция, сюръекция и биекция

Пусть f: А ® В. Тогда функция f называется:

инъективной, если b = f (a₁) & b = f (a₂) 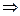a₁ = a₂,

сюрьективной, если " b Î B $ а Î A b = f (а);

биективной, если она инъективная и сюръективная.

ТЕОРЕМА Если f: А ® В — тотальная биекция (fа = А), то отношение f^{- 1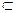} В ´ А (обратная функция) является биекцией.

Определения

Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности. Обычно отношение эквивалентности обозначают знаком º.

Пример

Отношения равенства чисел и множеств являются отношениями эквивалентно­сти. Отношение равномощности множеств также является отношением эквива­лентности.

Антисимметричное транзитивное отношение называется отношением порядка. Отношение порядка может быть рефлексивным, и тогда оно называется отноше­нием нестрогого порядка. Отношение порядка может быть антирефлексивным, и тогда оно называется отношением строгого порядка. Отношение порядка мо­жет быть полным (линейным), и тогда оно называется отношением полного, или линейного порядка. Отношение порядка может не обладать свойством полноты (линейности), и тогда оно называется отношением частичного порядка.

Обычно отношение строгого порядка (полного или частичного) обозначается знаком <, а отношение нестрогого порядка — знаком <. Отношение порядка в общем случае обозначается знаком .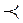

Пример

Отношение < на множестве чисел является отношением строгого полного поряд­ка. Отношение < на множестве чисел является отношением нестрогого полного порядка. Отношение Ì на булеане 2 ^м является отношением нестрогого частич­ного порядка.

Множество, на котором определено отношение частичного порядка, называется частично упорядоченным. Множество, на котором определено отношение полного порядка, называется вполне упорядоченным.

Пример

Множество чисел упорядочено линейно, а булеан упорядочен частично.

Дата добавления: 2014-12-27