
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исчисление предикатов
|
|
|
|
Определения
Для упрощения структуры сложных логических рассуждений введем специальные обозначения для некоторых часто встречающихся выражений. Условимся обозначать выражение “для всякого x свойство R выполнено” как  x R (x), а выражение “существует по крайней мере один x, обладающий свойством (предикатом) R ” – как
x R (x), а выражение “существует по крайней мере один x, обладающий свойством (предикатом) R ” – как  x R (x). В выражениях
x R (x). В выражениях  x R (x) и
x R (x) и  x R (x) обозначения
x R (x) обозначения 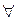 x и
x и  x будем соответственно называть квантором всеобщности и квантором существования.
x будем соответственно называть квантором всеобщности и квантором существования.
(Чистое) исчисление предикатов (первого порядка) – это формальная теория K, в которой определены следующие компоненты:
| связки | основные | Ø ® |
| дополнительные | & 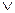
| |
| служебные символы | (,) | |
| кванторы | всеобщности | " |
| существования | $ | |
| предметные | константы | a, b, …,a 1, b 1, … |
| переменные | x, y, …,x 1, y 1, … | |
| предметные | предикаты | P, Q, … |
| функторы | f, g, … |
С каждым предикатом и функтором связано некоторое натуральные число, которое называется арностью или местностью.
<формула>::= <атом>|
Ø<формула>|
(<формула>®<формула>)|
"<переменная> <формула>|
$<переменная> <формула>
<атом>::= <предикат> (<список терминов>)
<список терминов>::= <терм> | <терм>, <список терминов>
<терм>::= <константа> |
<переменная> |
<функтор>(< список терминов>)
Пример
" x (Р (х)® $ у Q (x, y))
Логическое следование и логическая эквивалентность
Формула В является логическим следствием формулы А (обозначение: А 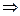 В), если формула В выполнена на любом наборе в любой интерпретации, на котором выполнена формула А. Формулы А и В логически эквивалентны (обозначение: А=В), если они являются логическим следствием друг друга. Имеют место следующие логические следования и эквивалентности:
В), если формула В выполнена на любом наборе в любой интерпретации, на котором выполнена формула А. Формулы А и В логически эквивалентны (обозначение: А=В), если они являются логическим следствием друг друга. Имеют место следующие логические следования и эквивалентности:
1. 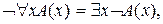

2. 

3. 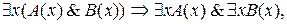
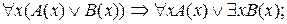
4. 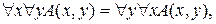

5. 

6. 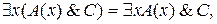
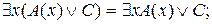
7. 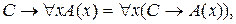

8. 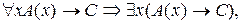
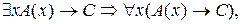
где формула С не содержит никаких вхождений переменной х.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 371; Нарушение авторских прав?; Мы поможем в написании вашей работы!