
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические связки
|
|
|
|
Введение
Дискретная математика – это цикл математических наук, изучающих свойства конечных множеств.
В настоящее время эти науки бурно развиваются, что определяется тремя очень важными факторами:
1) развитием компьютерной техники и компьютерных наук, которые базируются, а по существу являются продолжением дискретной математики;
2) запросами различных прикладных наук – теории управления, экономики, оптимизации и многих, многих других;
3) логикой внутреннего развития этих наук: появлением новых разделов, глубоких интересных проблем, развитием мощных методов их решения.
Глава 1. Логические исчисления
Высказывания
Элементами логических рассуждений являются утверждения, которые либо истинны, либо ложны, но не то и другое вместе. Такие утверждения называются (простыми) высказываниями. Простые высказывания обозначаются пропозициональными переменными, принимающими истинностные значения «И» (или 1) и ложные значения «Л» (или 0). Из простых высказываний с помощью логических связок могут быть построены составные высказывания. Обычно рассматривают следующие логические связки:
| Название | Прочтение | Обозначение |
| Отрицание Конъюнкция Дизъюнкция Импликация Эквивалентность | не и или если... то равносильно | Ø,  &, Ù, ×
Ú
®, Þ
«, Û, ~, =, º
&, Ù, ×
Ú
®, Þ
«, Û, ~, =, º
|
Формулы
Правильно построенные составные высказывания называются (пропозициональными) формулами. Формулы имеют следующий синтаксис:
(формула):: = И | Л |
<пропозициональная переменная> |
(Ø <формула>) |
(<формула> & <формула>) |
(<формула> 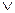 <формула>) |
<формула>) |
(<формула> ® <формула>)|
(<формула> «<формула>)
Для упрощения записи вводится старшинство связок (Ø, &, 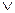 , ®, «) и лишние скобки опускаются.
, ®, «) и лишние скобки опускаются.
Истинностное значение формулы определяется через истинностные значения ее составляющих в соответствии со следующей таблицей:
| A | B | Ø A | А & В | A 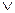 B B
| A  B B
| A «B |
| Л | Л | И | Л | Л | И | И |
| Л | И | И | Л | И | И | Л |
| И | Л | Л | Л | И | Л | Л |
| И | И | Л | И | И | И | И |
Интерпретация
Пусть A (x 1, ..., xn) — пропозициональная формула, где х 1 ,.… хn — входящие в нее пропозициональные переменные. Конкретный набор истинностных значений, приписанных переменным x 1, ...,xn, называется интерпретацией формулы А. Формула может быть истинной (иметь значение И) при одной интерпретации и ложной (иметь значение Л) при другой интерпретации. Значение формулы А в интерпретации I будем обозначать I (А). Формула, истинная при некоторой интерпретации, называется выполнимой. Формула, истинная при всех возможных интерпретациях, называется общезначимой (или тавтологией). Формула, ложная при всех возможных интерпретациях, называется невыполнимой (или противоречием).
Пример
А 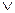 Ø A — тавтология, А & ØА — противоречие, A
Ø A — тавтология, А & ØА — противоречие, A  ØА - выполнимая формула, она истинна при I (А) = Л.
ØА - выполнимая формула, она истинна при I (А) = Л.
ТЕОРЕМА Пусть А — некоторая формула. Тогда:
1. если А — тавтология, то Ø A — противоречие, и наоборот;
2. если А — противоречие, то  А — тавтология, и наоборот;
А — тавтология, и наоборот;
3. если А — тавтология, то неверно, что А — противоречие, но не наоборот;
4. если А — противоречие, то неверно, что А — тавтология, но не наоборот.
Логическое следование и логическая эквивалентность
Говорят, что формула В логически следует из формулы А (обозначается А 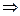 В), если формула В имеет значение И при всех интерпретациях, при которых формула А имеет значение И.
В), если формула В имеет значение И при всех интерпретациях, при которых формула А имеет значение И.
Говорят, что формулы A и В логически эквивалентны (обозначается А 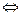 В или просто А = В), если они являются логическим следствием друг друга. Логически эквивалентные формулы имеют одинаковые значения при любой интерпретации.
В или просто А = В), если они являются логическим следствием друг друга. Логически эквивалентные формулы имеют одинаковые значения при любой интерпретации.
ТЕОРЕМА (Р  Q)=(Ø P
Q)=(Ø P 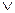 Q).
Q).
Доказательство
Для доказательства достаточно проверить, что формулы действительно имеют одинаковые истинностные значения при всех интерпретациях:
| Р | Q | P  Q Q
| Ø Р | Ø p 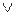 q q
|
| И | И | И | Л | И |
| Л | И | И | И | И |
| И | Л | Л | Л | Л |
| Л | Л | И | И | И |
ТЕОРЕМА Если А, В, С — любые формулы, то имеют место следующие логические эквивалентности:
1. 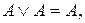
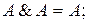
2. 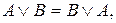
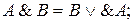
3. 
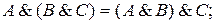
4. 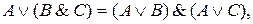
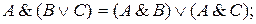
5. 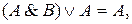
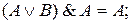
6. 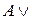 Л= A,
Л= A,  Л=Л;
Л=Л;
7. 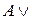 И=И,
И=И,  И=A;
И=A;
8. 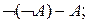
9. 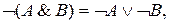
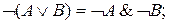
10. 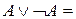 И,
И, 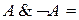 Л.
Л.
Доказательство
Непосредственно проверяется построением таблиц истинности.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 423; Нарушение авторских прав?; Мы поможем в написании вашей работы!