
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исчисление высказываний
|
|
|
|
Классическое определение исчисления высказываний
Исчисление высказываний — это формальная теория L, в которой:
1. Алфавит: Ø и  — связки;
— связки;
(,) — служебные символы;
а, b,..., a 1, b 1,... — пропозициональные переменные.
2.Формулы: 1) переменные суть формулы;
2) если А, В — формулы, то (ØA) и (A  В) — формулы.
В) — формулы.
3. Аксиомы: A 1: (А  (В
(В  A));
A));
A 2: ((A  (В
(В  С))
С))  ((A
((A  В)
В)  (A
(A  С)));
С)));
A 3: ((Ø В  Ø A)
Ø A)  ((Ø В
((Ø В  A)
A)  В)).
В)).
4. Правило 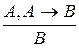 .
.
Здесь А и В — любые формулы. Таким образом, множество аксиом теории L бесконечно, хотя задано тремя схемами аксиом. Множество правил вывода также бесконечно, хотя оно задано только одной схемой
При записи формул лишние скобки опускаются, если это не вызывает недоразумений. Другие связки вводятся определениями (а не аксиомами):
A & B = Ø (A  Ø B),
Ø B),
A Ú В = Ø A  В.
В.
Любая формула, содержащая эти связки, рассматривается как синтаксическое сокращение собственной формулы теории L.
Производные правила вывода
ТЕОТЕМА  L A
L A  A
A
Доказательство
1.  по
по 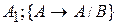
2. 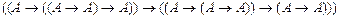 по
по 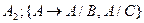
3. 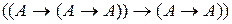 из пунктов 1,2
из пунктов 1,2
4. 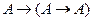 по
по 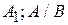
5. 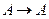 из пунктов 4,3
из пунктов 4,3
ТЕОРЕМА А  L В
L В 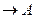
Доказательство
1. A гипотеза
2. 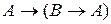 по A 1
по A 1
3. 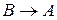 из пунктов 1,2
из пунктов 1,2
Всякую доказанную выводимость можно использовать как новое (производное) правило вывода. Например, последняя доказанная выводимость называется правилом введения импликации.
Дедукция
В теории L импликация очень тесно связана с выводимостью.
ТЕОРЕМА (дедукции) Если Г, А  L В, то Г
L В, то Г  L А ® В и обратно.
L А ® В и обратно.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!