Определения графов

Упражнения

1. Проверить приведенные в теории равносильности путем построения таблиц ис­тинности.

2. Построить СДНФ для х ₁ | х ₂, х ₁¯ х ₂.

3. Минимизировать булеву функцию f (x ₁, x ₂, x ₃) = Ø(x ₁ Ú x ₁Ø x ₂) ® Ø x ₁ x ₂ x ₃, используя равносильности, операции склеивания и поглощения.

4. Минимизировать следующие функции с помощью диаграмм Вейча: f (x ₁, x ₂) = Ø x ₁ x ₂ ® x ₂, f (x ₁, x ₂, x ₃) = x ₁ ® Ø x ₂ Ú Ø x ₁Ø x ₂(x ₃ Å Ø x ₁), f (x ₁, x ₂, x ₃, x ₄) = Ø x ₁ x ₂ ® (x ₄ ¯ x ₃).

5. Проверить принадлежность классам Т ₀, Т ₁, T_*, T _<, Т_L функций ¯, |, Ú, ®, Å.

6. Определить

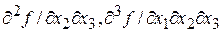для функции f (x ₁, x ₂, x ₃) = x ₁ ® Ø x ₁Ø x ₂(x ₃ Å Ø x ₁).

Глава 6. Графы

Основное определение

Графом G (V, E)называется совокупность двух множеств — непустого множества V (множества вершин)и множества Е неупорядоченных пар различных элемен­тов множества V (Е — множество ребер).

G (V, E) = (V; E), V ¹ Æ, E Ì V ´ V, E = E ^-1.

Число вершин графа G обозначим р, а число ребер — q:

p = p (G) = | V |, q = q (G) = | E |.

Смежность

Пусть v ₁, v ₂ — вершины, е = (v₁, v₂) — соединяющее их ребро. Тогда вершина v ₁ и ребро е инцидентны, вершина v ₂ и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается Г⁺(v):

Г⁺(v) = {u Î V | (u, v) Î E},

Г(v) = Г⁺(v) 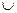{ v },

и Î Г(v) Û v Î Г(u).

Диаграммы

Обычно граф изображают диаграммой:вершины — точками (или кружками), ребра — линиями (рисунок 6.1, а).

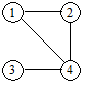а)

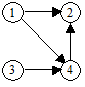б)

Рис. 6.1. Диаграммы графов

Другие определения

Часто рассматриваются следующие родственные графам объекты.

1. Если элементами множества Е являются упорядоченные пары, то граф назы­вается ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества Е — дугами. (пример диаграммы орграфа приведен на рисунке 6.2, б)

2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф назы­вается графом с петлями (или псевдографом).

3. Если Е является не множеством, а набором, содержащим несколько одинако­вых элементов, то эти элементы называются кратными ребрами, а граф назы­вается мулътиграфом.

4. Если элементами множества Е являются не обязательно двухэлементные, а любые подмножества множества V, то такие элементы множества Е называ­ются гипердугами, а граф называется гиперграфом.

5. Если задана функция F: V ® М и/или F: Е ® М, то множество М называ­ется множеством пометок, а граф называется помеченным (или нагруженным). В качестве множества пометок обычно используются буквы или целые числа.

Изоморфизм графов

Говорят, что два графа G ₁(V ₁, E ₁)и G ₂(V ₂, E ₂) изоморфны (обозначается G₁ ~ G₂), если существует биекция h: V ₁ ® V ₂, сохраняющая смежность:

e ₁ = (u, v) Î E ₁Þ е ₂ = (h (u), h (v))Î Е₂,

е ₂ = (u, v)Î E ₂ Þ e ₁ = (h ^-1(u), h ^-1(v))Î E₁.

Пример

Три внешне различные диаграммы, приведенные на рис. 6.2, являются диаграм­мами одного и того же графа К _{3, 3.}

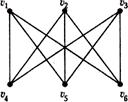
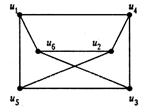
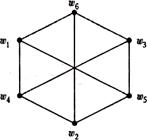
Рис. 6.2.Диаграммы изоморфных графов

Дата добавления: 2014-12-27