Понятие Хи-квадрата

Связь двух номинальных переменных с двумя значениями.

Тема 15. Анализ связей между номинальными переменными

1. Связь двух номинальных переменных с двумя значениями. Понятие Хи-квадрата.

2. Связь двух номинальных переменных, имеющих больше двух значений.

3. Связь между несколькими номинальными переменными.

Напомним, чем отличается описательное исследование от аналитического. В первом случае мы строим перечневые таблицы и графики и получаем представление о ситуации в целом. Например, мы можем выяснить на основании табл. 15.1, что примерно половина респондентов (45,4%) характеризуют состояние медицинского обслуживания положительно, а другая половина респондентов (47,4%) характеризуют состояние медицинского обслуживания отрицательно (см. анализ такой таблицы в теме 12).

Таблица 15.1

Как Вы сегодня оцениваете состояние медицинского обслуживания? (Переменная X)	Абс. числа	%
1. Положительно		10,5
2. Скорее положительно, чем отрицательно		34,9
3. Скорее отрицательно, чем положительно		31,7
4. Отрицательно		15,7
5. Затрудняюсь ответить		7,1

Мы выясняем также, что чуть больше 40% респондентов в случае появления проблем со здоровьем, обратятся в первую очередь к родственникам, друзьям и знакомым, а чуть больше трети респондентов в такой же ситуации обратятся в поликлинику по месту жительства (табл. 15.2).

Таблица 15.2

В случае появления проблем со здоровьем, к кому Вы обратитесь в первую очередь?(Переменная Y)	Абс. числа	%
К родственникам, друзьям, знакомым, имеющим опыт такого же рода недомоганий.		42,1
В поликлинику по месту жительства.		35,7
Затрудняюсь ответить.		21,0

При аналитическом же исследовании нас интересуют связи между ответами различных подгрупп респондентов. И важно, чтобы эти связи были статистически значимыми.

Мы, например, можем сделать напрашивающееся предположение, что из той подгруппы респондентов, которые в целом отрицательно оценивают состояние медицинского обслуживания, значительная часть, скорее всего, выбрала ответ, что в сложной ситуации они обратятся к родственникам, друзьям и знакомым. Далее мы можем попробовать подтвердить или опровергнуть это предположение, используя различные коэффициенты связи, а на следующем шаге выяснить, насколько величина полученного коэффициента связи между двумя переменными – «оценка состояния медицинского обслуживания» и «куда обратиться в случае появления проблем со здоровьем» – является статистически значимой, т. е. неслучайной.

Проделаем это. Для начала рассмотрим таб. 15.3.

Таблица 15.3

Переменная Х	Переменная Y	Всего
Y 1	Y 2
Х 1	a	b	a + b
Х 2	c	d	c + d
Всего	a + c	b + d	a + b + c + d

В этой таблице соотносятся две переменные X и Y, каждая из которых имеет два значения: X ₁ и X ₂ и Y ₁ и Y ₂. Буквы a, b, c, d обозначают данные, которые будут проставлены в ячейках при реальном исследовании:

a – число респондентов, выбравших одновременно вариант ответа Х ₁ и вариант ответа Y ₁,

b – число респондентов, выбравших одновременно вариант ответа Х ₁ и вариант ответа Y ₂,

c – число респондентов, выбравших одновременно вариант ответа Х ₂ и вариант ответа Y ₁,

d – число респондентов, выбравших одновременно вариант ответа Х ₂ и вариант ответа Y ₂.

Таким образом, мы построили макет таблицы 2х2.

При помощи такой таблицы связь между двумя переменными можно определять двояким способом: через коэффициент Юла или коэффициент Пирсона. Вот их формулы:

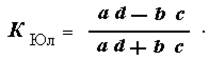
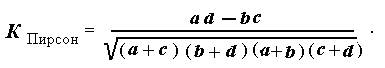
Используя данные, на основе которых строилась сводная таблица об оценках состояния медицинского обслуживания, строим по образцу табл. 15.3 табл. 15.4, вписывая вместо букв a, b, c, d соответствующие числа.

В ячейке a мы поместили число тех респондентов, которые положительно оценивают состояние медицинского обслуживания, но в случае появления проблем со здоровьем обратятся тем не менее за помощью к родственникам, друзьям или знакомым.

Таблица 15.4

Оценка состояния медицинского обслуживания, X	Куда обратятся в случае проблем со здоровьем, Y	Итого
К родств., друзьям, знакомым, Y 1	В поликлинику, Y 2
Положительно + скорее положительно, чем отрицательно, X 1	180, a	275, b	455, a + b
Скорее отрицательно, чем положительно + отрицательно, X 2	322, c	142, d	464, c + d
Итого	502, a + c	417, b + d	919, a + b + c + d

В ячейке b – число респондентов, которые положительно оценивают состояние медицинского обслуживания и в случае проблем со здоровьем обратятся в поликлинику по месту жительства. В ячейке c – число респондентов, которые в общем отрицательно оценивают состояние медицинского обслуживания и в случае проблем со здоровьем обратятся к родственникам, друзьям, знакомым. И наконец, в ячейке d – число респондентов, которые отрицательно оценивают состояние медицинского обслуживания, но тем не менее в случае проблем со здоровьем обратятся в поликлинику по месту жительства.

Обратим внимание, что в итоговых ячейках (они называются маргиналами) получились несколько иные числа, чем соответствующие абсолютные числа в табл. 15.1 и 15.2. Дело в том, что определенную часть данных по переменной X забрал на себя ответ «Затрудняюсь ответить» при переменной Y, а определенную часть данных по переменной Y забрал на себя ответ «Затрудняюсь ответить» при переменной X.

Теперь рассчитаем коэффициент Юла:

К _Юла = (180х142 – 275х322): (180х142 + 275х322) = (25560 – 88550): (25560 + 88550) = –62990: 114110 = –0,55.

Считается, что связь является значимой, если значение коэффициента Юла выходит за пределы ±0,5. Знак плюс означает, что имеется связь между значениями переменных X ₁ и Y ₁, а также X ₂ и Y ₂. Знак минус означает наличие связи между значениями переменных X ₂ и Y ₁, и X ₁ и Y ₂.

У нас коэффициент получился 0,55 со знаком минус. Содержательно это означает, что среди тех, кто оценивает состояние медицинского обслуживания скорее отрицательно, чем положительно, или отрицательно, сравнительно больше тех, кто в случае появления проблем со здоровьем обратится скорее к родственникам, друзьям, знакомым. И соответственно, среди тех, кто оценивает состояние медицинского обслуживания положительно или скорее положительно, чем отрицательно, сравнительно больше тех, кто в случае сложной ситуации обратится в поликлинику по месту жительства.

В принципе мы получили довольно предсказуемый вывод. Конечно, отрицательно оценивающие состояние медицинского обслуживания и должны, скорее всего, обращаться к помощи друзей и родственников. Но, во-первых, эта предсказуемость вывода означает, что наша анкета валидна и результатам нашего опроса в целом можно верить.

И во-вторых, самое главное – мы измерили количественно связь между обеими переменными. Коэффициент равен –0,55, то есть не слишком выходит за пределы –0,5. А ведь коэффициент мог быть равен –0,9, и на основании такого коэффициента пришлось бы намечать оргвыводы в отношении департамента здравоохранения региона.

Теперь выясним, каким при тех же данных окажется коэффициент Пирсона. _______________

К _Пирсон = (180х142 – 275х322): √ 502х417х455х464 = –62990:

___________

√44194594080 = –62990: 210255 = –0,3.

Когда использовать коэффициент Юла, а когда Пирсона? Коэффициент Юла проще, потому что четко намечена граница существенной связи: ±0,5. Но он неудобен в случае, если хотя бы в одной из клеток таблицы имеется очень малое по сравнению с остальными число. Тогда числитель и знаменатель в формуле будут близкими по величине и коэффициент автоматически будет стремиться к ±1, но необязательно из-за того, что связь очень высокая. Поэтому коэффициент Юла удобно применять, когда значения переменных в исходных таблицах делятся примерно поровну.

Так, в табл. 15.2 переменная «Куда обратятся в случае проблем со здоровьем» делится между двумя значениями в соотношении 42,1 и 35,7%, т. е. значениями более или менее близкими. И в табл. 15.1 сумма положительных значений (10,5 + 34,9 = 45,4) и сумма отрицательных значений (31,7 + 15,7 = 47,4) тоже примерно равны. Если же нет этого примерного равенства и есть перекос в значениях, то при дополнительном разделении данных в ячейках таблицы 2х2 могут оказаться слишком малые числа, и тогда использование коэффициента Юла будет затруднительным.

С другой стороны, считается, что коэффициент Пирсона более надежен, так как его статистическую значимость можно проверить при помощи так называемого Хи-квадрата.

Итак, как определить, много это или мало в данном случае, когда коэффициент Пирсона равен 0,3? Вообще, он может меняться от +1 до –1. А если равен нулю, значит, связи нет.

Чтобы определить это «много или мало», мы строим таблицу 2х2 с такими данными, при которых точно отсутствует связь между переменными. И затем сравниваем реальную и построенную таблицы. Это сравнение происходит через так называемый Хи-квадрат.

Хи-квадрат символически обозначается χ². Формула Хи-квадрата следующая:

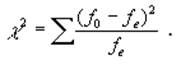
Здесь f₀ – фактические числа в каждой ячейке таблицы, кроме маргиналов. Например, в нашей таблице это числа 180, 275, 322, 142.

f_e – числа, ожидаемые в соответствующих ячейках, при условии, что между переменными X и Y отсутствует какая-либо связь.

Посмотрим, как определять f_e.

Обозначим маргинал a + b как S _{X 1}, маргинал c + d – как S _X2, a + c – как S _{Y 1}, b + d – как S _{Y 2} и сумму a + b + c + d – как S _{X Y}. Тогда получаем следующие формулы для заполнения ячеек таблицы:

Как видим, чтобы определить ожидаемое число в определенной ячейке, нужно перемножить маргиналы при данной ячейке и разделить на сумму всех случаев.

Определяем: a = 248,5; b = 206,5; c = 254,4; d = 210,5.

Мы можем проверить правильность наших расчетов: a + b = 248,5+206,4 = 455; Аналогично можно проверить, получатся ли маргиналы 464, 502, 417.

Строим табл. 15.5, вставляя числа, соответствующие a, b, c, d.

Таблица 15.5

Оценка состояния медицинского обслуживания, X	Куда обратятся в случае проблем со здоровьем, Y	Всего
К родств., друзьям, знакомым, Y 1	В поликлинику, Y 2
Положительно + скорее положительно, чем отрицательно, X 1	248,5 a	206,5, b	a + b
Скорее отрицательно, чем положительно + отрицательно, X 2	253,5 c	210,5 d	c + d
Всего	502, a + c	417, b + d	a + b + c + d

Так должна выглядеть таблица, если бы не было связи между оценкой состояния медицинского обслуживания и тем, куда граждане собираются обращаться в случае проблем со здоровьем.

Теперь возвращаемся к определению Хи-квадрата. Строим табл. 15.6.

Таблица 15.6

Определение χ² по шагам

f0	fe	f0 – fe	(f0 –fe)^2	(f0 –fe)^2 fe
	248,5	–68,5	4692,25	18,88
	206,5	68,5	4692,25	22,72
	253,5	68,5	4692,25	18,51
	210,5	–68,5	4692,25	22,3
Сумма	82,41

Итак, Хи-квадрат получился равным 82,41. Кстати, в третьей колонке получились числа, отличающиеся только знаком. Это свойство таблицы 2х2.

Теперь нам нужно сравнить полученный Хи-квадрат с Хи-квадратом, который соответствует отсутствию статистически значимой связи между переменными. Итак, насколько число 82,41 статистически значимо?

Сначала необходимо определить степень свободы для таблицы 2х2.Степень свободы – то количество ячеек таблицы, которые достаточно заполнить, чтобы определить содержание остальных ячеек при данных маргиналах. Формула для определения степеней свободы такова:

df = (r – 1) х (c – 1),

здесь r – количество заполненных строк по горизонтали, а с – количество заполненных столбцов (кроме маргиналов). В нашем случае таблица состоит из двух строк и двух столбцов, поэтому df = (2 – 1)х(2 – 1) = 1.

Если бы таблица состояла из трех строк и двух столбцов, то степень свободы равнялась бы: (3 − 1)х(2 − 1) = 2.

Теперь можно оценить статистическую значимость полученного коэффициента Пирсона при помощи таблицы распределения Хи-квадрата (табл. 15.7). Более полный вариант таблицы распределения Хи-квадрата представлен в Приложении.

Таблица 15.7

Распределение χ²

df	0,05	0,01	0,001
1 2 3 4 5	3,841 5,991 7,815 9,488 11,070	6,635 9,210 11,345 13,277 15,086	10,827 13,815 16,266 18,467 20,515

Таблица содержит минимальные величины χ², соответствующие наличию значимой связи для различных степеней свободы на уровнях 0,001; 0,01; 0,05. Уровень 0,001 означает, что мы рискуем ошибиться один раз из 1000, соответственно уровни 0,01 и 0,5 означают вероятность ошибиться один раз из 100 и пять раз из 100.

Мы видим, что значение полученного нами χ² (82,41) значительно превышает при степени свободы, равной единице, то, что указано в таблице даже для уровня 0,001. Это значит, что взаимосвязь, которую мы определили при помощи коэффициента Пирсона, статистически значима и мы можем быть уверены, что имеем дело с закономерностью.

Почему нам при определении величины коэффициента связи между переменными дополнительно нужно еще определять Хи-квадрат и сравнивать его с Хи-квадратом на таблице? Мы определяем Хи-квадрат при данном коэффициенте и при данной величине выборки. Если бы выборка была меньше, то даже при том же самом коэффициенте связи Хи-квадрат мог оказаться меньше того, что указан в таблице. И тогда при такой выборке данный коэффициент указывал бы лишь на наличие случайной связи.

Проделаем опыт. Пусть у нас будет та же исходная таблица 2х2, но с величиной выборки в 35 раз меньше, т. е. респондентов будет не 919, а 26. Строим табл. 15.8, в клетках которой все данные тоже будут уменьшены примерно в 35 раз.

Таблица 15.8

Оценка состояния медицинского обслуживания, X	Куда обратятся в случае проблем со здоровьем, Y	Итого
К родств., друзьям, знакомым, Y 1	В поликлинику, Y 2
Положительно + скорее положительно, чем отрицательно, X 1
Скорее отрицательно, чем положительно + отрицательно, X 2
Итого

Определяем коэффициент Пирсона.

___________

К _Пирсон = (5х4 – 8х9): √14х12х13х13 = (20 – 72): √28392 = 52: 168,5 = –0,31.

Итак, мы получили коэффициент связи, примерно равный прежнему, –0,3.

Теперь строим таблицу 15.9, используя формулы с маргиналами, в клетках которой будут числа, соответствующие отсутствию связи между обеими переменными.

Таблица 15.9

Оценка состояния медицинского обслуживания, X	Куда обратятся в случае проблем со здоровьем, Y	Итого
К родств., друзьям, знакомым, Y 1	В поликлинику, Y 2
Положительно + скорее положительно, чем отрицательно, X 1
Скорее отрицательно, чем положительно + отрицательно, X 2
Итого

Строим табл. 15.10 для определения Хи-квадрата.

Мы видим, что получившийся Хи-квадрат отличается от минимального Хи-квадрата в меньшую сторону (3,84 и 2,48). Это различие означает, что связь, выражаемая коэффициентом –0,31, теперь, при выборке, равной всего 26 респондентам, нельзя считать статистически даже при почти тех же самых коэффициентах связи.

Таблица 15.10

Определение χ² по шагам

f0	fe	f0 – fe	(f0 –fe)^2	(f0 –fe)^2 fe
		–2		0,57
				0,67
				0,57
		–2		0,67
Сумма	2,48

Итак, Хи-квадрат позволяет определить, с какой вероятностью полученный коэффициент выражает неслучайную связь при данной величине выборки.

Вывод: при разных объемах выборки один и тот же коэффициент может выражать связь разной степени случайности. Чем больше объем выборки, тем меньший по величине коэффициент связи может оказаться статистически значимым. И наоборот, даже большой по величине коэффициент связи, но при малом объеме выборки, может не оказаться статистически значимым.

Дата добавления: 2014-12-27