Определение связи между двумя порядковыми переменными

Тема 16. Анализ связи между порядковыми переменными

1. Определение связи между двумя порядковыми переменными.

2. Определение связи между таблицами с порядковыми переменными.

Допустим, мы хотим выяснить, насколько согласуются две порядковые переменные, причем пусть обе переменные имеют небольшое количество значений. Для этого вернемся к результатам конкурса красоты среди школьниц, представленным в теме 12. Напомним, что четыре школьницы сравнивались по трем переменным: грациозность походки, обаятельность и умение поддержать беседу. См. табл. 16.1.

Таблица 16.1

Результаты конкурса красоты среди старшеклассниц школы № …

Претендентки	Характеристики	Сумма балов
Грациозность походки	Обаятельность	Умение поддержать беседу
Ольга
Светлана
Марина
Наташа

Так как сравниваются показатели четырех школьниц, то это означает, что каждая из трех переменных имеет всего четыре значения, например, переменная «грациозность походки» имеет значения: 5, 8, 9, 6.

В случае, когда переменные изменяются по небольшому числу значений, можно использовать коэффициент ранговой корреляции Гудмана, который в литературе еще называют коэффициентом «гамма».

Попробуем выяснить при помощи этого коэффициента, существует ли связь между оценками за грациозность походки и оценками за обаятельность. То есть можно ли сказать, что более грациозной походке соответствует и большая обаятельность. Для этого расставим ранги (места) в порядке убывания по первой переменной (А) и сопоставим с ними места по второй переменной (В) (табл. 16.2).

Таблица 16.2

Результаты конкурса красоты среди старшеклассниц школы № …

Претендентки	Характеристики	Ранги по А	Ранги по В
Грациозность походки, А	Обаятельность, В
Марина
Светлана
Наташа
Ольга

Проведем попарное сравнение рангов (см. табл. 16.3), выясняя, совпадают или не совпадают порядки между рангами. Если порядки совпадают, ранги будем называть согласованными и обозначать знаком плюс,если порядки не совпадают, то такую пару рангов будем считать несогласованной и обозначать знаком минус. Знаки > и < будут соответственно означать «занимать более высокое место» и «занимать более низкое место».

Таблица 16.3

Попарное сравнение рангов двух переменных

Пары	Сравнение рангов по грациозности походки	Сравнение рангов по обаятельности	Согласованность, несогласованность
Марина – Светлана	1 > 2	1 > 3	+
Марина – Наташа	1 > 3	1 > 2	+
Марина – Ольга	1 > 4	1 > 4	+
Светлана – Наташа	2 > 3	3 < 2	–
Светлана – Ольга	2 > 4	3 > 4	+
Наташа – Ольга	3 > 4	2 > 4	+

Формула определения связи такова:

где n ₊ – число согласованных пар, n _–– число несогласованных пар.

Ясно, что коэффициент g может изменяться от 0 до ±1. Считается, что при коэффициенте, равном или больше 0,5, между двумя порядковыми переменными имеется согласованность. При коэффициенте, равном нулю, между переменными отсутствует какая-либо связь, и если коэффициент менее –0,5, речь идет о противоположности порядков между переменными.

В нашем примере g = (5 – 1): (5 + 1) = 4: 6 = 0,667. Получается, что между оценками за грациозность походки и за обаятельность имеется существенная согласованность, так как коэффициент больше 0,5.

Теперь посмотрим, существует ли связь между оценками за грациозность походки и за умение поддержать беседу. Строим соответствующие табл. 16.4 и 16.5.

Таблица 16.4

Результаты конкурса красоты среди старшеклассниц школы № …

Претендентки	Характеристики	Ранги по А	Ранги по В
Грациозность походки, А	Умение поддержать беседу, В
Марина
Светлана
Наташа
Ольга

Таблица 16.5

Попарное сравнение рангов двух переменных

Пары	Сравнение рангов по грациозности походки	Сравнение рангов по обаятельности	Согласованность +, несогласованность –
Марина – Светлана	1 > 2	1 > 4	+
Марина – Наташа	1 > 3	1 > 2	+
Марина – Ольга	1 > 4	1 > 3	+
Светлана – Наташа	2 > 3	4 < 2	–
Светлана – Ольга	2 > 4	4 < 3	–
Наташа – Ольга	3 > 4	2 > 3	+

Подчитываем по формуле: g = (4 – 2): (4 + 2) = 2: 6 = 0,33.

Получается, что значимая связь между оценками за грациозность походки и за умение поддерживать беседу отсутствует, так как соответствующий коэффициент меньше 0,5.

Можно предположить, что умение поддерживать беседу не обязательно сочетается с грациозностью походки.

Представляем читателю самостоятельно выяснить, имеется ли согласованность между оценками за обаятельность и способность поддерживать беседу.

Рассмотрим случай, когда сравниваемые порядковые переменные имеют много значений и соответственно число строк в исходной таблице достаточно велико. Тогда более удобно использовать коэффициент ранговой корреляции Спирмена. Он вычисляется по формуле:

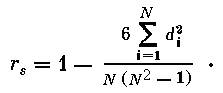
Здесь d _i – разность между рангами в одной и той же строке; N – количество строк; S – знак суммы.

Читается так: коэффициент равен единице минус сумма квадратов разностей между рангами, умноженная на 6 и деленная на произведение количества строк на разность между квадратом количества строк и единицей.

Величина r _s может изменяться в преде­лах от +1 до –1. При коэффициенте, равном 1, порядок рангов обеих переменных полностью согласуется между собой, при коэффициенте –1 порядок рангов полностью противоположен. При коэффициенте, равном нулю, имеем беспорядочное расположение рангов.

Рассмотрим на примере. Допустим, нас продолжают интересовать результаты исследования оценки гражданами работы органов здравоохранения. Поставим вопрос, есть ли существенное отличие между респондентами до 40 лет включительно и респондентами старше 40 лет в понимании того, что будет способствовать улучшению работы органов здравоохранения. Обращаемся к табл. 16.6.

В таблице 7 строк, т. е. переменные А и В имеют по 7 значений. Если бы мы определяли коэффициент ранговой корреляции способом, указанным выше, нам пришлось бы строить таблицу, в которой сравнивались 21 ситуация (6 + 5 + 4 + 3 + 2 + 1) с проверкой на согласованность рангов. Это оказалось бы довольно громоздким делом.

Таблица 16.6

Что, по Вашему мнению, будет способствовать улучшению работы органов здравоохранения?	Респонденты до 40 лет, А	Респонденты старше 40 лет, В	Ранг по А	Ранг по В	di	di ^2
Улучшение технической оснащенности медицинских учреждений
Установление общественного контроля за деятельностью органов здравоохранения
Борьба с поборами под видом подарков лечащему персоналу
Увеличение заработной платы работникам медицины
Постоянное повышение квалификации работников медицины
Усиление ответственности за неправильное лечение граждан
Организация специализированных центров по сложным видам заболеваний
Всего

Теперь действуем прямо по формуле:

r _s= 1 – 6 х 18: (7 х (49 – 1)) = 1 – 6 х 18: (7 х 48) = 1 – 0,32 = 0,68.

Итак, коэффициент равен 0,68. Можно сказать, что между респондентами моложе 40 и старше 40 лет все же имеется определенное согласие в том, что должно способствовать улучшению работы органов здравоохранения. Следует отметить, что если при сравнивании обнаруживается много объединенных рангов (см. об объединенных рангах в теме 4), то формула Спирмена неприменима[32].

Определим статистическую значимость полученного коэффициента по таблице критических величин r _s (см. табл. 16.7). Полностью эта таблица дается в Приложении настоящего учебного пособия (табл. 5).

Мы видим, что коэффициент 0,68 в седьмой строке превышает критическое значение r _s лишь на уровне 0,1, которому соответствует величина 0,571. Уровень 0,1 означает возможность 1 ошибки на 10 случаев, что не так уж мало.

Делаем вывод: нельзя утверждать уверенно, что имеется согласованность между мнениями респондентов до 40 лет и старше 40 лет относительно мер улучшения работы органов здравоохранения.

Таблица 16.7

Критические значения коэффициента ранговой корреляции Спирмена r _s (фрагмент)

Количество строк	Уровни значимости
0,10	0,05	0,025	0,01	0,005
n – 4	1,000	l,000
	0,800	0,900	1,000	1,000
	0,657	0,829	0,886	0,943	1,000
	0,571	0,714	0,786	0,893	0,929
	0,524	0,643	0,738	0,833	0,881
	0,483	0,600	0,700	0,783	0,833
	0,455	0,564	0,648	0,745	0,794

Дата добавления: 2014-12-27