
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Смысл коэффициента корреляции Пирсона
|
|
|
|
Вернемся к коэффициенту Пирсона. Чтобы лучше понять его роль, проведем эксперимент. Увеличим разброс точек вдоль прямой. Для этого в столбце, соответствующем переменной Y, в первой строке уменьшим на 2 число часов, проводимых перед телевизором, во второй строке число часов, наоборот, увеличим на 2, в третьей строке снова уменьшим на 2, в четвертой – увеличим на 2 и т. д. Получаем табл. 17.5.
Таблица 17.5
| № | ||||||||||||||||||||
| X | ||||||||||||||||||||
| Y | 6,5 | 1,5 |
Этой таблице соответствует график на рис. 17.4, в котором все точки разбросаны, если можно так выразиться, с большим размахом.
Интересно здесь то, что уравнение линии регрессии при новом, более размашистом положении точек, оказывается практически тем же самым, и, соответственно, почти тем же самым является коэффициент связи.
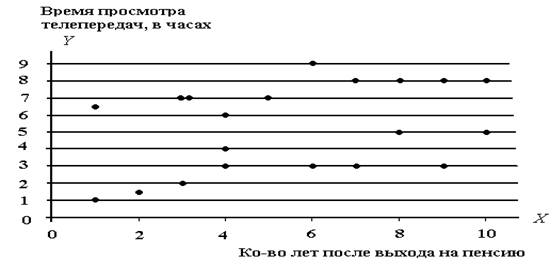
Рис. 17.4. Время, затрачиваемое на просмотр телепередач, при различных количествах лет, прошедших после выхода на пенсию (второй вариант)
Покажем это. Строим табл. 17.6, в которой сведены элементы формулы
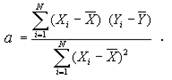
Таблица 17.6
| № | 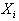
| 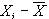
| 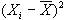
| 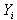
| 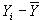
| 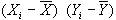
|
| –4,5 | 20,25 | –4,25 | 19,125 | |||
| –4,5 | 20,25 | 6,5 | 1,25 | –5,625 | ||
| –3,5 | 12,25 | 1,5 | –3,75 | 13,125 | ||
| –2,5 | 6,25 | 1,75 | –4,375 | |||
| –2,5 | 6,25 | –3,25 | 8,125 | |||
| –2,5 | 6,25 | 1,75 | –4,375 | |||
| –1,5 | 2,25 | –2,25 | 3,375 | |||
| –1,5 | 2,25 | 0,75 | –1,125 | |||
| –1,5 | 2,25 | –1,25 | 1,875 | |||
| –0,5 | 0,25 | 1,75 | –0,875 | |||
| 0,5 | 0,25 | –2,25 | –1,125 | |||
| 0,5 | 0,25 | 3,75 | 1,875 | |||
| 1,5 | 2,25 | –2,25 | –3,375 | |||
| 1,5 | 2,25 | 2,75 | 4,125 | |||
| 2,5 | 6,25 | –0,25 | –0,625 | |||
| 2,5 | 6,25 | 2,75 | 6,875 | |||
| 3,5 | 12,25 | –2,25 | –7,875 | |||
| 3,5 | 12,25 | 2,75 | 9,625 | |||
| 4,5 | 20,25 | –0,25 | –1,125 | |||
| 4,5 | 20,25 | 2,75 | 12,375 | |||
| S = 110 | S = 161 | S = 105 | S = 50 | |||
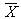 = 5,5 = 5,5
| 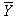 = 5,25 = 5,25
|
Получаем: а = 0,31 (50: 161); в = 3,5 (5,25 – 0,31 х 5,5).
Новое уравнение: Y = 0,31 X + 3,5. Мы видим, что оно почти совпадает с прежним уравнением: Y = 0,286 X + 3,68.
Итак, коэффициент связи между обеими переменными может практически не измениться даже при большем разбросе точек.
Теперь проверим коэффициент 0,31 на статистическую значимость, для этого определим коэффициент корреляции Пирсона. Напоминаем его формулу:
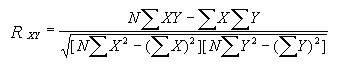
Снова строим таблицу, в которой присутствуют необходимые элементы формулы (табл. 17.7).
Таблица 17.7
| № | x | y | xy | x 2 | y 2 |
| 6,5 | 6,5 | 42,25 | |||
| 1,5 | 2,25 | ||||
| S = 110 | S = 105 | S = 636,5 | S = 776 | S = 719,5 |
Определяем коэффициент Пирсона:
_________________________________
R xy = (20х636,5 – 11550): √(20х776 - 12100) х (20х719,5 – 11025) =
____________________________ _________
= (12730 – 11550): √(15520 – 12100) х (14390 – 11025) = 1180: √3420 х 3365 = 1180: √11508300 = 1180: 3392,4 = 0,348.
Выбираем уровень значимости 0,05, количество степеней свободы равно 18, в таблице коэффициента корреляции (табл. 17.4) этим данным соответствует число 0,4438. У нас же получилось 0,348. Следовательно, наш новый коэффициент связи 0,31 не является статистически значимым. Уравнением Y = 0,31 X + 3,5 мы выразили всего лишь случайную связь.
Даже если бы мы претендовали на 1 ошибку в 10 случаях, наш коэффициент связи все равно являлся бы статистически незначимым, так как таблица коэффициента корреляции дает в этом случае число 0,3783, которое больше получившегося у нас коэффициента Пирсона.
Сделаем вывод. Увеличение разброса точек снижает вероятность получения статистически значимого коэффициента связи между переменными. Можно сказать иначе, коэффициент Пирсона измеряет степень близости точек к линии, выражающей связь между интервальными переменными.
Проведя соответствующие расчеты, несложно показать, что в случае, когда все точки лежат точно на прямой, коэффициент Пирсона равен единице.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!