Проверка коэффициента связи на статистическую значимость

Мы справились с первой задачей – измерили количественно зависимость между обеими переменными. Теперь необходимо решить вторую задачу: убедиться в том, что найденный коэффициент 0,286 статистически значим.

Снова, не вдаваясь в математические тонкости, дадим формулу, по которой проверяется статистическая значимость полученного коэффициента связи. Это так называемый коэффициент корреляции Пирсона, обозначим его R _xy.

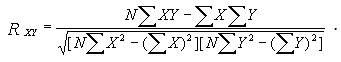
Строим таблицу, в которой присутствуют все необходимые элементы уже этой формулы (табл. 17.3).

Опираясь на данные таблицы, производим вычисления:

________________________________

R _xy = (20 х 623,5 – 11550): √(20 х 776 – 12100) х (20 х 575,5 – 11025) =

____________________________

= (12470 – 11550): √(15520 – 12100) х (11510 – 11025) =

_________ _______

= 920: √3420 х 485 = 920: √1658700 = 920: 1287,9 = 0,714.

Итак, R _xy = 0,714.

Таблица 17.3

№	x	y	xy	x ^2	y ^2
		4,5	4,5		20,25
		3,5			12,25
	S = 110	S = 105	S = 623,5	S = 776	S = 575,5

Теперь можно выяснить, является ли коэффициент связи 0,286 статистически значимым. Для этого сначала нужно определить количество степеней свободы. Оно определяется по формуле N − 2, где N − количество случаев. У нас N = 20. Поэтому количество степеней свободы равно 18 (20 − 2). Теперь нужно определиться с желательным уровнем значимости. Пусть он будет 0,05, что означает, что для нас достаточно ошибиться в 5 случаях из 100.

Смотрим на фрагмент таблицы коэффициентов корреляции для различных уровней значимости (табл. 17.4), полный вариант этой таблицы см. в Приложении настоящего учебного пособия, табл. 6.

Таблица 17.4

df	0,1	0,05	0,01	0,001
16 17 18 19 20	0,4000 0,3887 0,3783 0,3687 0,3598	0,4683 0,4555 0,4438 0,4329 0,4227	0,5897 0,5751 0,5614 0,5487 0,5368	0,7084 0,6932 0,6787 0,6652 0,6524

Уровню значимости 0,05 и количеству степеней свободы 18 в таблице соответствует число 0,4438. Получившийся у нас коэффициент Пирсона 0,714 больше этого числа. Следовательно, для уровня значимости 0,05 коэффициент связи (0,286) является статистически значимым. То есть своим уравнением прямой Y = 0,286 X + 3,68 мы выразили не случайную, но значимую связь.

Но даже если бы мы претендовали на 1 ошибку в 1000 случаях, то наш коэффициент все равно являлся бы статистически значимым, так как таблица дает в этом случае число 0,6787, которое все равно меньше получившегося у нас коэффициента Пирсона.

Опираясь на полученное выше уравнение Y = 0,286 X + 3,68, можно представить, вокруг какого числа будут крутиться, если можно так выразиться, точки, указывающие на количество часов просмотра телепередач, у респондентов, вышедших на пенсию 15 лет назад.

Подставляем 15 вместо X в уравнение Y = 0,286 X + 3,68.

Получаем: 0,286 х 15 + 3,68 = 7,97.

Итак, средний мужчина в возрасте 75 лет должен, по нашим данным, высиживать перед телевизором примерно 8 часов в сутки.

А в возрасте 80 лет, т. е. на 20-м году после выхода на пенсию? Тоже можно подсчитать: 0,286х20 + 3,68 = 9,4.

Правда, так можно досчитаться до того, что в 100-летнем возрасте мужчина в среднем будет прикован к телевизору больше 15 часов в сутки, отводя на сон, еду и прочие потребности меньше 9 часов. Но ясно, что наши математические расчеты имеют границу в виде здравого смысла.

Дата добавления: 2014-12-27