Статистическое планирование эксперимента. Выбор параметра оптимизации и независимых факторов. Построение матриц полного факторного эксперимента

Получение математических моделей процессов резания МЕТОДОМ ПОЛНОГО факторного эксперимента

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Под планированием эксперимента понимают постановку опытов по заранее составленной схеме, которая имеет определённые свойства. При этом все исследуемые факторы изменяют одновременно, а влияние неизвестных или не включённых в исследования факторов рандомизируют с помощью особых статистических приёмов.

Получение математических моделей методом полного факторного эксперимента (ПФЭ) осуществляется в следующей последовательности:

1 Выбор параметра оптимизации;

2 Выбор вида математической модели;

3 Выбор интервала варьирования факторов;

4 Построение матрицы ПФЭ;

5 Проведение эксперимента;

6 Получение математической модели;

7 Проверка адекватности математической модели.

Характеристика цели исследования, заданная количественно, называется параметром оптимизации или критерием оптимальности. Параметр оптимизации является результатом изучаемого процесса, его выходом или реакцией откликом.

Параметр оптимизации должен удовлетворять таким требованиям:

1 Быть эффективным с точки зрения достижения конечной цели исследований;

2 Быть доступным для измерений;

3 Быть статистически эффективным.

Задача планирования экспериментов формулируется математически таким образом: необходимо иметь некоторое представление о поверхности откликов факторов, которую в общем случае можно представить в виде функции или математической модели:

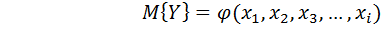, (1.1)

где Y- параметр оптимизации;

x_i- переменные факторы.

Таким образом, задача заключается в нахождении зависимости математического ожидания результата выхода процесса от независимых факторов. Модель должна быть адекватной, то есть способные прогнозировать результаты эксперимента с заданной точностью. Очень часто при описании процессов ограничиваются моделью, которая содержит линейные члены и взаимодействия первого порядка:

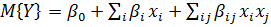, (1.2)

где 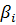- теоретические коэффициенты регрессии.

Используя для получения математической модели результаты эксперимента, можно определить только выборочные коэффициенты регрессии b₀, b_i, b_ij, которые являются оценками для теоретических коэффициентов регрессии, то есть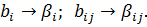

Таким образом, уравнение регрессии, полученное на основе результатов экспериментов, отличается от теоретического и имеет вид:

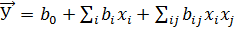, (1.3)

где 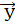– оценка математического ожидания .

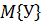Каждый фактор, участвующий в процессе, имеет определенные границы изменения своей величины, где он может принимать любые значения, или ряд дискретных значений. Совокупность всех значений, которые может принимать данный фактор, называется зоной определения фактора. Однако, в зоне определения необходимо найти локальную часть для планирования эксперимента, т.е. для каждого фактора необходимо узнать тот интервал изменения, в пределах которого выполняют эксперимент. Для этого на основе априорной информации устанавливают ориентировочные значения факторов, комбинация которых дает наилучший результат. В этой комбинации значения факторов соответствует многомерная точка в факторном пространстве, которую и принимает за исходную точку при построении плана эксперимента. Координаты этой точки называются основными (нулевыми) уровнями факторов.

Интервалом варьирования фактора называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний уровень фактора. Величина этого интервала принимается на единицу нового масштаба измерения фактора.

Для упрощения записи условий эксперимента и обработки результатов эксперимента масштаба выбирают так, чтобы верхний уровень соответствовал (+1), нижний (-1), а основной соответствовал 0.

Минимально необходимое число уровней факторов определяется максимальным порядком интерполяционного полинома по данному фактору. Оно должно быть на единицу больше этого порядка. Наиболее часто планирование на двух уровнях, которое позволяет описать процесс полиномиальной линейной моделью, которая содержит и взаимодействие факторов.

Экспериментальные планы, у которых все факторы варьируются на двух уровнях, называется планами типа 2^k, где k- число факторов.

Полным факторным экспериментом называется эксперимент, который всевозможные неповторяющиеся комбинации уровней независимых (4)факторов, каждый из которых варьируется на двух уровнях. Число таких комбинаций .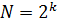

Рассмотрим поучение математической модели для трехфакторной задачи. Уравнение регрессии в этом случае имеет вид

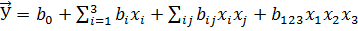. (1.4)

Получение модели методом ПФЭ осуществляется в следующей последовательности:

- планирование эксперимента;

- выполнение самого эксперимента;

- проверка однородности выборочных дисперсий;

- получение математической модели с проверкой статистической значимости выборочных коэффициентов регрессии;

- проверка адекватности математической модели.

Используя кодовые значения факторов (+1,-1), условия эксперимента можно записать в виде таблицы или матрицы планирования эксперимента, где строки соответствуют различным опытам, а столбцы – значениям факторов. Матрица ПФЭ для трех факторов приведена в таблице 1.1.

Таблица 1.1 – Матрица планирования эксперимента 2³ и результаты исследований

№ Точки плана v	X0	X1	X2	X3	X1X2	X1X3	X2X3	X1X2X3	Параметры оптимизации Y
	+	-	-	-	+	+	+	-	Y1
	+	+	-	-	-	-	+	+	Y2
	+	-	+	-	-	+	-	+	Y3
	+	+	+	-	+	-	-	-	Y4
	+	-	-	+	+	-	-	+	Y5
	+	+	-	+	-	+	-	-	Y6
	+	-	+	+	-	-	+	-	Y7
	+	+	-	+	+	+	+	+	Y8

Для удобства построения матриц планов типа 2^k существует три приема, один из которых основа на правиле чередования знаков. Столбцы Х₀ все знаки (+), в столбце Х₁ знаки чередуются через один, в столбце Х₂ – через два, в столбце Х₃ –через четыре т.е. по степеням числа 2. Знаки других столбцов получают перемножением.

Дата добавления: 2014-12-27