Получение математической модели зависимости температуры резания от элементов режимов резания

Лабораторная работа №1

Цель работы – получить математическую модель зависимости температуры резания от элементов режима резания с использованием полного факторного эксперимента типа 2³.

Оборудование, приборы, инструменты, заготовки.

1 Токарно - винторезный станок мод. 16К20

2 Термопары

3 Резцы с заданными постоянными характеристиками

4 Гальванометр

5 Изоляционные прокладки.

Содержание и порядок выполнения работы

1 В лабораторных условиях при продольном точении стали резцами НхВ=25х25мм (материал режущей части Т5К10, геометрические параметры: ). Проводят ПФЭ типа 2³ с целью получения зависимости температуры резания от глубины резания t, подачи S и скорости резания V. Для измерения температуры резания используют метод естественной термопары.

2 Для каждой переменной (фактора) выбирают два уровня её изменения: верхний (+1) и нижний (-1). Каждому фактору присваивают соответствующее кодовое обозначение: V=x₁, S=x₂, t=x₃. Значения факторов приведены в таблице 1.4.

Таблица 1.4- Уровни независимых факторов

Уровень	Значения факторов
V(x1) м/мин.	П, мин^-1	S(x2), мм/об	T(x3), мм.
Нижний (-1)			0,07	0,5
Нулевой (0)			0,16	1,25
Верхний (+1)			0,26	2,0

3 Строят матрицу ПФЭ (таблица 1.5). Для каждого опыта определяют термо-э.д.с., которую с помощью тарировочных графиков переводят в температуру резания. Минимальное количество опытов N=2³=8. Для исключения влияния различных случайных факторов проводят рандомизацию опытов (при их трёхкратном повторении). Результат опытов заносят в таблицу 1.5.

4 Математическая модель зависимости температуры резания от элементов режима резания должна быть получена в виде:

(1.15)

где - постоянный коэффициент, учитывающий физико-механические свойства материала заготовки и условия обработки;

x, y, z – показатели степеней.

Для получения степенных зависимостей используют логарифмические масштабы. После логарифмирования обеих частей формулы (1.15) и введения членов, учитывающих взаимодействия факторов, уравнение регрессии будет иметь вид:

Y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃+b₁₂₃x₁x₂x₃, (1.16)

где Y- логарифм температуры резания;

b₀,b₁,b₂… - коэффициенты регрессии;

х_1,x_2,x₃- соответственно логарифмы скорости резания V, подачи S и глубины резания t.

5 Для расчёта коэффициентов регрессии используют столбцы матрицы ПФЭ и логарифмы средних значений температуры резания .

6 Коэффициенты регрессии b_i рассчитывают по формулам:

(1.17)

7 Дисперсию, характеризующую ошибку опыта, рассчитывают по формуле (1.7).

8 Дисперсию параметра оптимизации Y рассчитывают по формуле (1.8).

9 Проводят оценку однородности дисперсии по 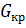Кохрена по формуле (1.9). Если дисперсия не однородна то в точке плана с максимальной дисперсией выполняют повторные опыты. Расчеты повторяют с использованием вновь полученных значений .

10 Рассчитывают дисперсию коэффициента регрессии по формуле (1.10).

11 Выполняют проверку значимости коэффициентов регрессии по Стьюдента (формула (1.11)).

12 С учетом значимых коэффициентов Записывают полученные уравнения регрессии и используют его для расчета (значения по полученной модели). Результаты расчета записывают в таблицу 1.5.

13 Рассчитывают дисперсию адекватности (формула 1.12).

14 Проводят проверку адекватности полученной модели по критерию Фишера (формула 1.14).

15 Переход от кодированных значений , , к натуральным переменным (элементам режима резания) осуществляют по формулам:

(1.18)

Таблица 1.5 – Матрица ПФЭ типа 2³ и результаты измерений температуры резания

№ опыта

V (x1), м/мин

n, мин^-1

S(x2), мм/об

t(x3), мм

Кодовые обозначения

Температура резания Y=Q

Дисперсия опыта

Значения по модели

х0

х1

х2

х3

х1х2

х1х3

х2х3

х1х2х3

y1V

lny1

y2V

lny2

y3V

lny3

Среднее

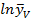
1, 9, 17

2, 10, 18

3, 11, 19

4, 12, 20

5, 13, 21

6, 14, 22

7, 15, 23

8, 16, 24

16 Значения , , выраженные формулами (1.18) подставляют в полученное уравнение регрессии. Для получения степенных зависимостей результат потенцируют.

Содержание отчета

1Наименование работы.

2 Цель работы.

3 Оборудование, приборы, инструменты, заготовки.

4 Схема измерения температуры резания.

5 Независимые факторы и уровни их изменения (таблица 1.4).

6 Матрица ПФЭ и результаты расчетов (таблица 1.5).

7 Результаты расчетов коэффициентов регрессии; дисперсии, характеризующих ошибку опыта и проверку однородности дисперсий по критерию Кохрена.

8 Результаты проверки значимости коэффициентов регрессии по критерию Стьюдента.

9 Результаты проверки адекватности математической модели.

10 Математическая модель.

11 Выводы.

Контрольные вопросы

1 В чем особенности полного фактического эксперимента.

2 Назовите требования к параметру оптимизации Y.

3 Как выбирают независимые факторы и уровни их изменения.

4 Как определяют минимальное количество опытов при полном фактическом эксперименте?

5 С какой целью выполняют повторные опыты?

6 Как строят матрицы полного фактического эксперимента?

7 С какой целью выполняют проверку однородности эксперимента?

8 Как и по какому критерию проверяют однородность дисперсии?

9 По какому критерию проверяют значимость коэффициентов регрессии?

10 Что характеризует дисперсия адекватности?

11 Как осуществляют проверку адекватности математической модели?

Дата добавления: 2014-12-27