
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оборудование, приборы, инструменты, заготовки
|
|
|
|
Лабораторная работа №3
Получение математических моделей зависимости износа образцов от величины и времени приложения нагрузки
Цель работы – получить математические модели зависимости износа образцов из стали Р6М5 и образцов из стали Р6М5 упрочненных импульсным магнитным полем (Р6М5+ОИМП) от величины и времени приложения нагрузки с использованием полного факторного эксперимента типа 22.
1 Прибор ЭХО-1.
2 Образцы из стали Р6М5 и Р6М5, упрочненных импульсным магнитным полем (Р6М5+ОИМП).
3 Набор грузов.
4 Инструментальный микроскоп.
Содержание и порядок выполнения работы
1 В лабораторных условиях при моделировании износа на приборе ЭХО-1проводят ПФЭ типа 22 с целью получения математической модели зависимости износа (диаметра отпечатка d) от времени приложения (τ) и величины нагрузки (p).
2 Для каждой переменной (фактора) выбирают два уровня ее измерения: верхний (+1) и нижний (-1). Каждому фактору присваивают соответствующее кодовое значение: τ=х1, Р=х2, d=x2, d=y. Значения факторов приведены в таблице 1.10.
Таблица 1.10 – Уровни независимых факторов
| Уровень | Значение факторов | |
| τ (х1), с | Р(х2), кг | |
| Нижний (-1) | 0,155 | |
| Нулевой (0) | 0,203 | |
| Верхний (+1) | 0,250 |
3 Строят матрицы ПФЭ для образцов из стали Р6М5 и (Р6М5+ОИМП) (таблица 1.11, 1.12). Минимальное количество опытов N=22=4. Для исключения влияния различных случайных факторов проводят рандомизацию опытов (при их трехкратном повторении). Методика получения диаметров отпечатков приведена в п. 1.2.1. Результаты опытов заносят в таблицу 1.11 и 1.12.
4 Математическая модель износа образцов от величины и времени приложения нагрузки должна быть получена в виде
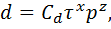 (1.23)
(1.23)
где 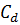 – постоянный коэффициент, учитывающий свойства образцов и условий испытаний;
– постоянный коэффициент, учитывающий свойства образцов и условий испытаний;
x, z – показатели степеней.
Для получения степенных зависимостей используют логарифмические масштабы. После логарифмирования обеих частей формулы (1.23) и ведения членов, учитывающих взаимодействие факторов, уравнение регрессии будет иметь вид
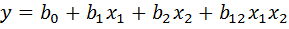 , (1.24)
, (1.24)
где 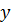 – логарифм диаметра отпечатка;
– логарифм диаметра отпечатка;
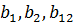 – коэффициент регрессии;
– коэффициент регрессии;
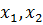 – логарифмы времени и величины нагрузки.
– логарифмы времени и величины нагрузки.
5 Для расчета коэффициентов регрессии используют столбцы матрицы ПФЭ и логарифмы средних значений диаметров отпечатков ( ). В качестве примера можно использовать расчеты по формуле (1.17).
). В качестве примера можно использовать расчеты по формуле (1.17).
6 Дисперсию, характеризующую ошибку опыта, рассчитывают по формуле (1.7).
7 Дисперсию параметра оптимизации у рассчитывают по формуле (1.8).
8 Проводят оценку однородности дисперсий по Gкр. Кохрена по формуле (1.9). Если дисперсии не однородны, то в точке плана с максимальной дисперсией выполняют повторные опыты. Расчеты повторяют с использованием вновь полученных значений  .
.
9 Рассчитывают дисперсию коэффициента регрессии по формуле (1.10).
10 Выполняют проверку значимости коэффициентов регрессии по tкр. Стьюдента (формула 1.11).
11 С учетом значимых коэффициентов bi записывают полученное уравнение регрессии и используют его для расчета 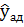 (значений
(значений  по модели). Результаты расчетов записывают в таблицы 1.11, 1.12.
по модели). Результаты расчетов записывают в таблицы 1.11, 1.12.
12 Рассчитывают дисперсию адекватности (формула 1.12).
13 Производят проверку адекватности полученной модели по критерию Фишера (формула 1.14).
Таблица 1.11 – Матрица ПФЭ типа 22 и результаты измерений диаметров отпечатков (образцы из стали Р6М5)
| № опыта |  , с , с
| 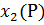 , кГ , кГ
| x0 | x1 | x2 | x1x2 | Текущие значения у | Средние у | Дисперсия опыта 
| Значение по нормали 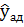
| ||||||
| у1 | ln у1 | у2 | lnу2 | у3 | lnу3 | 
| 
| |||||||||
| 1,5,9 | 0,155 | + | - | - | + | 57,5 | 60,0 | 62,5 | ||||||||
| 2,6,10 | 0,155 | + | + | - | - | 70,7 | 72,5 | 75,0 | ||||||||
| 3,7,11 | 0,250 | + | - | + | - | 80,8 | 83,0 | 85,0 | ||||||||
| 4,8,12 | 0,250 | + | + | + | + | 95,0 | 100,0 | 98,0 |
Таблица 1.12 – Матрица ПФЭ типа 22 и результаты измерений диаметров отпечатков (образцы из стали Р6М5+ОИМП)
| № опыта |  , с , с
| 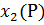 , кГ , кГ
| x0 | x1 | x2 | x1x2 | Текущие значения у | Средние у | Дисперсия опыта 
| Значение по нормали 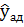
| ||||||
| у1 | ln у1 | у2 | lnу2 | у3 | lnу3 | 
| 
| |||||||||
| 1,5,9 | 0,155 | + | - | - | + | 42,5 | 40,0 | 40,0 | ||||||||
| 2,6,10 | 0,155 | + | + | - | - | 52,5 | 50,0 | 55,0 | ||||||||
| 3,7,11 | 0,250 | + | - | + | - | 65,0 | 60,0 | 65,0 | ||||||||
| 4,8,12 | 0,250 | + | + | + | + | 80,0 | 85,0 | 90,0 |
14 Переход от кодированных значений х1 и х2 к натуральным переменным τ и Р осуществляют по формулам

(1.25)
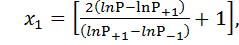
15 Значения х1 и х2, выраженные формулами (1.25) подставляют в полученные уравнения регрессии. Для получения степенных зависимостей результаты потенцируют.
Содержание отчета
1 Наименование работы.
2 Цель работы.
3 Оборудование, приборы, инструменты, заготовки.
4 Схемы измерения диаметра отпечатка.
5 Независимые факторы и уровни их измерения (таблица 1.10).
6 Матрицы ПФЭ и результаты расчетов диаметров отпечатков и их логарифмов для образцов из стали Р6М5 и (Р6М5+ОИМП) (таблицы 1.11, 1.12).
7 Результаты расчетов коэффициентов регрессии; дисперсии, характеризующей ошибку опыта, и проверки однородности дисперсий по критерию Кохрена.
8 Результаты проверки значимости коэффициентов регрессии по критерию Стьюдента.
9 Результаты проверки адекватности математических моделей.
10 Математические модели износа для различных образцов.
11 Выводы.
Контрольные вопросы
1 Назовите возможности метода моделирования процесса износа и рекомендуемые области его применения.
2 Назовите порядок получения математических моделей методом ПФЭ.
3 Что характеризует адекватность м атематической модели и по какому критерию ее проверяют?
4 Как определяют области изменения независимых факторов τ и Р?
5 Назовите отличия математических моделей износа для различных видов образцов.
6 Позволяет ли метод моделирования процесса износа получить адекватные модели при различных физико-механических свойствах исследуемых образцов?
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 547; Нарушение авторских прав?; Мы поможем в написании вашей работы!