Отображения линей­ных пространств

Норма и скалярное произведение векторов.

Линейная (не)зависимость векторов. Базисы. Размерность линеала.

Линейные (векторные) пространства.

Квадратичные формы.

Определение и классификация квадратичных форм. Приведение к диагональному виду. Метод Лагранжа. Сигна­тура. За­кон инерции квадратичных форм. Нера­венства, определяющие знак квадратичной фор­мы.. Одновременное приведение к диагональному виду двух квадра­тичных форм. Приложения: критерий типа кри­вых и поверхностей второго порядка. Приведе­ние к каноническому виду. Примеры квадратич­ных форм в физике.

Аксиомы линейного пространства. Абстрактное понятие вектора. Примеры: множество рациона­льных чисел как линейное пространство; мно­жество действительных чисел как линейное про­странство; пространства R² и R ⁿ для любого n; множество всех действительных кусочно-непре­рывных функций, заданных на отрезке; множе­ство полиномов степени не вы­ше n; множества параллельных плоскостей в трехмерном евкли­довом пространстве. Множество комплексных чисел как линейное пространство.

Понятие линейной комбинации векторов. Три­виальная линейная комбинация. Определение линейной (не)зависимости. Некоторые критерии линейной (не)зависимости. Определение базиса. Ортонормированный базис.

Размерность линейного пространства.

Единственность разложения вектора по задан­но­му базису. Замена базиса.

Понятие гомоморфизма линейных пространств. Изоморфизм линейных пространств. Преобразо­вание базиса как преобразование изоморфизма. Норма вектора. Нормированные пространства. Примеры.

Скалярное произведение векторов. Виды опре­делений скалярного произведения векторов. Ли­нейные скалярные произведения. Свертка и ска­лярное произведение. Вещественное евклидово скалярное произведение. Строгое определение вещественного евклидова пространства. Орто­нормированные базисы­.

Линейные операторы. Представ­ление линейного оператора в заданных базисах. Примеры линей­ных операторов (преобразование базиса, опе­ратор проектирования, оператор про­из­водной). Представление ли­нейных операторов матрицами. Сумма линейных операторов. Умно­жение линейного оператора на число. Произве­дение линейных операторов. Степени линейных операто­ров..

Задача нахождения собственных значений и собственных векторов матрицы. Характеристиче­ское уравнение матрицы.

Ортогональный оператор. Приведение квадратичной формы к каноническому виду при помощи ортогонального преобразования.

Задача 1

Коллинеарны ли векторы 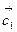и 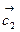, построенные по векторам 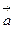и 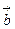, если:

1.

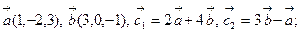
2.

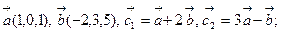
3.

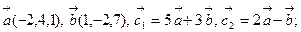
4.

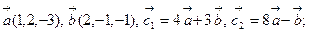
5.

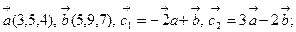
6.

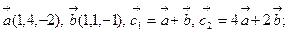
7.

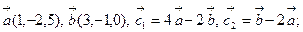
8.

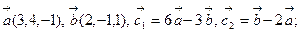
9.

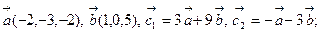
10.

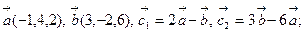
Задача 2

Вычислить объем тетраэдра с вершинами в точках A₁, A₂, A₃, A₄ и его высоту, опущенную из вершины A₄ на грань A₁A₂A₃, если:

1. A₁ (1,3,6), A₂ (2,2,1), A₃ (-1,0,1), A₄ (-4,6,-3);

2. A₁ (-4,2,6), A₂ (2,-3,0), A₃ (-10,5,8), A₄ (-5,2,-4);

3. A₁ (7,2,4), A₂ (7,-1,-2), A₃ (3,3,1), A₄ (-4,2,1);

4. A₁ (2,1,4), A₂ (-1,5,-2), A₃ (-7,-3,2), A₄ (-6,-3,6);

5. A₁ (-1,-5,2), A₂ (-6,0,-3), A₃ (3,6,-3), A₄ (-10,6,7);

6. A₁ (0,-1,-1), A₂ (-2,3,5), A₃ (1,-5,-9), A₄ (-1,-6,3);

7. A₁ (5,2,0), A₂ (2,5,0), A₃ (1,2,4), A₄ (-1,1,1);

8. A₁ (2,-1,-2), A₂ (1,2,1), A₃ (5,0,-6), A₄ (-10,9,-7);

9. A₁ (-2,0,-4), A₂ (-1,7,1), A₃ (4,-8,-4), A₄ (1,-4,6);

10. A₁ (14,4,5), A₂ (-5,-3,2), A₃ (-2,-6,-3), A₄ (-2,2,-1)

Задача 3

Проверить совместность системы и в случае совместности решить ее:

1) по формулам Крамера;

2) матричным методом;

3) методом Гаусса.

1. ;

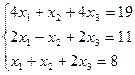2. ;

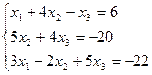3. ;

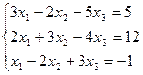4. ;

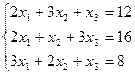5. ;

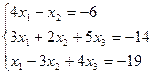6. ;

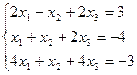7. ;

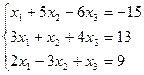8. ;

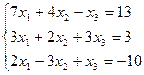9. ;

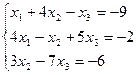10.

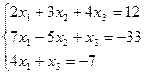
Задача 4

Решить однородную систему линейных уравнений:

1. ;

1. ;

1. ;

1. ;

1. ;

1. ;

1. ;

1. ;
2. ;

1. 

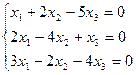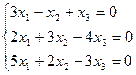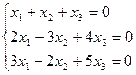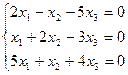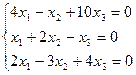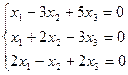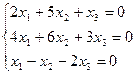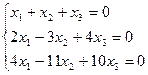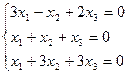Задача 5

Задан треугольник 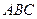координатами своих вершин. Найдите:

а) периметр треугольника;

б) точку пересечения медиан;

в) уравнение стороны ;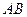

г) уравнение высоты, опущенной из вершины ;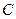

д) длину этой высоты.

1.	,	,	;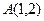
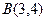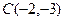2.	,	,	;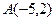
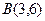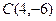3.	,	,	;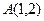
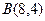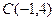4.	,	,	;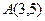
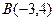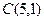5.	,	,	;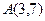
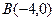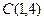6.	,	,	;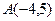
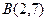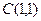7.	,	,	;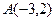
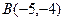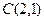8.	,	,	;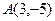
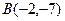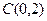9.	,	,	;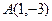
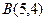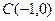10.	,	,	;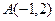

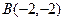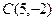Задача 6

Найти точку M ’, симметричную точке М относительно прямой;

1. M (0,-3,-2), ;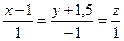

2. M (2,-1,1), ;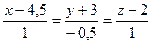

3. M (1,1,1), ;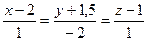

4. M (1,2,3), ;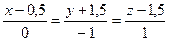

5. M (1,0,-1), ;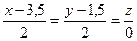

6. M (2,1,0), ;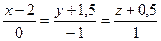

7. M (-2,-3,0), ;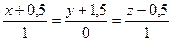

8. M (-1,0,-1), ;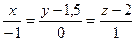

9. M (0,1,2), ;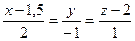

11. M (3,-3,-1),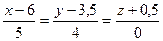

Задача 7

Составьте каноническое уравнение эллипса (для вариантов 1-15) или каноническое уравнение гиперболы (для вариантов 16-30), если:

1. Расстояние между фокусами равно 10, большая ось равна 26.

2. Большая ось равна 20, эксцентриситет .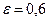

3. Расстояние между директрисами равно 18, большая ось равна 12.

4. Прямые 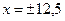являются директрисами, малая ось равна 12.

5. Точки 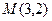, 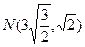принадлежат эллипсу.

6. Точка 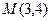принадлежит эллипсу, эксцентриситет .

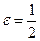7. Большая полуось равна 5, расстояние между фокусами равно 6.

8. Расстояния от фокуса до концов большой оси равны 1 и 9.

9. Сумма длин полуосей равна 8 и расстояние между фокусами равно 8.

10. Директрисы задаются уравнениями 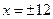, эксцентриситет .

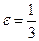Задача 8

Исследуйте данную поверхность методом сечений:

1.

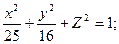
2. ;

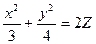3.

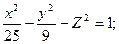
4.

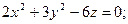
5.

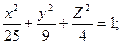
6.

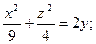
7.

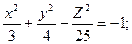
8.

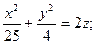
9.

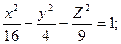
10.

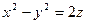
Литература

1. А. А. Гусак. Высшая математика. В 2-х т. Т.1- Мн.: ТетраСистемс, 2001.- 544с.

2. Р. Ф. Апатенок, А. М. Маркина, Н. В. Попова, В. Б. Хейнман. Элементы линейной алгебры и аналитической геометрии. - Мн.: Вышейшая школа, 1986.- 272с.

3. М. И. Клиот –Дашинский. Алгебра матриц и векторов. - СПб.: Изд-во «Лань», 2001.- 160 с.

4. Г. П. Размыслович и др. Сборник задач по геометрии и алгебре: Учебное пособие.- Мн.: Университетское, 1999 – 383 с.

5. Д. В Клетенник. Сборник задач по аналитической геометрии. – М.: Наука. Гл. ред. физ.- мат. лит., 1986. – 224 с.

6. А. А. Бурдун, Е. А. Мурашко, М. М. Толкачев, А. С. Феденко. Сборник задач по алгебре и аналитической геометрии. – Мн.: Университетское, 1999. – 302 с.

7. А. А. Гусак. Аналитическая геометрия и линейная алгебра: справочное пособие по решению задач.- Мн: ТетраСистемс, 2001.- 288 с.

Дата добавления: 2014-12-27