Ошибки измерений

Методы измерений

Числовая обработка результатов лабораторного эксперимента

Всякая лабораторная работа это эксперимент, при котором производится измерение той или иной величины. Если производят измерение, непосредственно сравнивая неизвестную величину с эталоном, то это будет метод непосредственного измерения. Например, измеряя длину стержня, вы сравниваете ее с эталоном – измерительной линейкой. Если непосредственно измерить величину не удается, то измерив какие-либо иные величины, связанные с неизвестной теми или иными законами, можно вычислить эту неизвестную величину. Так для того чтобы узнать величину сопротивления резистора измеряют силу тока I и напряжения U и по закону Ома () вычисляют сопротивление R.

Выделяют так же нулевой метод – метод, при котором влияние измеряемой величины компенсируют влиянием подобной же, но действующей в противоположном направлении. Этот метод используется при взвешивании тела с помощью разновесов: вес взвешиваемого тела компенсируется весом разновесов, так что общее действия тела и гирь на коромысло весов будет равняться нулю.

Точно определить какую-либо измеряемую величину не возможно. Допустим, необходимо измерить некую величину A. Точное значение нам неизвестно, но в результате n измерений этой величины мы получим ряд значений a₁,a₂… a_n, отличающихся от A на ∆a:

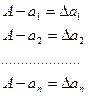(1)

называемые случайными ошибками измерений.

Сложив отдельно правые и левые части этих уравнений получим:

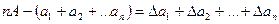, или (2)

Из теории вероятностей следует, что ошибки измерения лежат в пределах от −∆a до + ∆a. Отсюда можно предположить, что половина всех ошибок будет ∆a иметь положительную величину, а половина отрицательную. Тогда можно сумму всех ошибок приравнять нулю, т.е.: 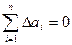, тогда уравнение (2) примет вид:

, (3), отсюда: 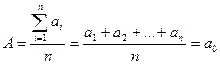(4)

Следовательно, за значение измеряемой величины можно принять среднее арифметическое a₀ из всех n измерений. Тогда равенство (1) примет вид:

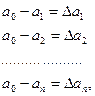(5)

где ∆a₁,∆a₂…∆a_n ошибки отдельных измерений.

Проводя эксперимент, во внимание принимается лишь абсолютное значение этих ошибок. Поэтому вычисляется величина средней арифметической ошибки среднего результата a₀: 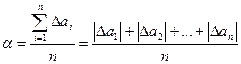(6)

Если число экспериментов велико, то вычисляют среднюю квадратичную ошибку средней арифметической величины a₀: (7)

Однако из теории вероятностей следует, что величину ошибок можно сузить, умножив среднюю квадратичную на 2/3. Тогда ошибка запишется следующим образом: 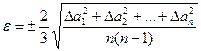(8)

Окончательный результат запишется в виде: (9)

Если число экспериментов не велико, что будет наблюдаться в большинстве случаев этого лабораторного практикума, то окончательный результат измерений можно записать в виде: 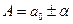(10)

Величина α или ε показывает, насколько истинное значение A измеряемой величины отличается от a₀, которую мы принимаем за A.

Абсолютная ошибка не дает представлений о точности эксперимента. Для определения точности используют относительную погрешность измерения средней арифметической величины. Она определяется как отношение средней арифметической ошибки к величине средней арифметической всех экспериментов. Чаще ее выражают в процентах: (11)

Дата добавления: 2014-12-27