Теоретическое введение. Колебательные движения.Колебаниями называются процессы, в которых одна или несколько основных физических величин являются периодическими или почти

Колебательные движения. Колебаниями называются процессы, в которых одна или несколько основных физических величин являются периодическими или почти периодическими функциями времени. В качестве примеров колебательных процессов можно привести суточные и годовые колебания температуры на Земле, электромагнитные колебания в колебательном контуре и т.п.

Фундаментальную роль играют гармонические колебания, происходящие по закону синуса или косинуса:

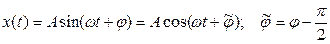, (1)

где х(t) – физическая величина, совершающая гармоническое колебание,

А, w, j – постоянные величины, характеризующие колебания.

График гармонического колебания представлен на рисунке 1.

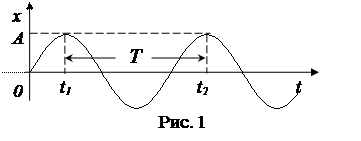Величина А>0 называется амплитудой колебания. В те моменты времени, когда sin(wt + j) = +1, переменная х(t) достигает своего максимального значения х_max=А. Следовательно, амплитуда гармонического колебания равна максимальному значению колеблющейся величины (часто ее обозначают той же буквой, что и саму переменную величину, помечая индексом х_max или х₀).

Три выражающиеся друг через друга физические величины характеризуют темп гармонического колебания: период Т, частота n (или f) и круговая, или циклическая частота w. Период Т - это время одного полного колебания (см. рис. 1). Частота, по определению, обратная периоду: 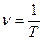(2). Она численно равна числу колебаний, совершаемых в единицу времени. Наиболее компактный вид формула гармонического колебания (1) имеет, если в ней фигурирует круговая частота w, которая связана с периодом Т соотношением:

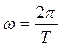. (3)

Действительно, для двух моментов времени t₁ и t₂, отстоящих на период (t₂ – t₁ = Т) (см. рис.1), значения аргумента синуса отличаются на 2p:

(wt₂ + j) – (wt₁ + j) = 2p, откуда w(t₂ – t₁) = 2p, т.е. w = 2p/Т.

Величина Ф(t) = wt + j, (4)

являющаяся аргументом синуса или косинуса в формуле гармонического колебания (1), называется фазой колебания. Она измеряется в радианах и характеризует стадию колебания. Например, при записи формулы колебания в синусоидальной форме (1) значениям фазы Ф=p/2+2pn (n – целое число) соответствуют моменты t достижения колеблющейся величиной максимального значения: х_max(t)=Asin(p/2+2pn)=A. Величина j определяет значение фазы в момент времени t=0: j=Ф(0), т.е. является начальной фазой. График, приведенный на рисунке 1, соответствует значению начальной фазы 0<j<p/2.

Колебания, которые возникают в системе, не подверженной действию внешних сил в результате какого-либо начального отклонения этой системы от состояния устойчивого равновесия, называют свободными. Если при колебаниях не происходит рассеяния энергии, то свободные колебания называются незатухающими. Простейший пример гармонического колебания - движения математического маятника.

Математический маятник. Тело, подвешенное на невесомой нерастяжимой нити, называется математическим маятником, если размеры тела пренебрежимо малы по сравнению с длиной нити (рис. 2). Если ограничиться рассмотрением малых колебаний в вертикальной плоскости, то математический маятник можно рассматривать как частный случай физического.На практике математическим маятником можно считать тяжелое тело, подвешенное на легкой нити, длина которой во много раз больше размеров тела. Если отклонить маятник из положения равновесия на не большой угол и затем отпустить его, то он начнет колебаться в вертикальной плоскости под действием собственного веса, плоскость колебаний не меняет свое положение при движении точки подвеса в пространстве.

Сила, возвращающая тело в состояние равновесия: F = mg×sina при малых углах a: 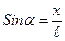, где x - смещение маятника из положения равновесия. 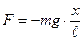(знак «-», т.к. сила направлена в сторону, противоположную смещению тела.), m, ℓ - постоянные для данного маятника. Сила F сообщает ускорение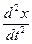 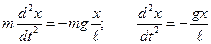. Обозначим 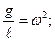w - угловая или циклическая частота. Тогда: 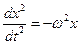- уравнение движения математического маятника.

Решения данного уравнения: x₁(t) = x = Asin(wt + j₀)

x₂(t) = x = Acos(wt + j₀)

Потенциальная энергия системы:

.

Если фаза изменяется на 2p, то значение величины x повторяется, прошедший интервал времени равен периоду Т.

w (t₂ - t₁) = 2p; t₂ - t₁ = T; wT = 2p;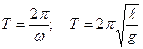

Из выражения для Т следует, что период зависит от длины маятника и ускорения свободного падения и не зависит от массы и амплитуды колебаний.

2.Описание лабораторной установки и метода измерения

Лабораторная установка (рис. 2.) состоит из двух шариков 1 (металлический и пластмассовый), закрепленных при помощи упругих нитей за держатели 2. Отклонение шариков от положения равновесия фиксируется сантиметровой линейкой 3.

3.Порядок выполнения работы

1. Выбирают один из маятников. Отводят шарик от положения равновесия на 10 см, отпускают шарик, предоставив ему свободно колебаться. В какой-либо момент наибольшего отклонения пускают в ход секундомер и отсчитывают время 30 полных колебаний.

2. Опыт повторяется три раза, каждый раз отсчитывая время 30 колебаний при амплитуде 10 см.

3. Далее шарик маятника отклоняется на 20 затем 30 см, каждый раз измеряя время 30 колебаний по три раза. Результаты заносятся в таблицу 1.

4. Выбирают два маятника с равной длинной подвеса ℓ, но с разной массой шариков и способом, указанным выше, измеряют время 30 колебаний обоих маятников поочередно. Опыт повторяется трижды для каждого из маятников. Результаты заносят в таблицу 2.

5. Выбирают один маятник и устанавливают определенную длину повеса ℓ и измеряют время 30 колебаний. Меняют длину подвеса и повторяют опыт. Результат заносят в таблицу 3.

4. Обработка результатов измерения

Таблица 1.

А, м	№	t, с	tср, с	n	Т, с

1. Проверить зависит ли период Т колебания математического маятника от амплитуды А колебаний. Для этого по формуле 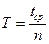, где t_ср (из таблицы 1) среднее значение времени 30 колебаний трех последовательных опытов для каждой из амплитуд. Результаты занести в таблицу 1

2. Сравнить периоды колебаний Т для разных значений амплитуд А.

3. Проверить зависит ли период колебаний Т математического маятника от массы m шарика. Для этого по формуле 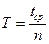, где t_ср (из таблицы 2) среднее значение времени 30 колебаний трех последовательных опытов для каждого из маятников с шариками разной массы. Результаты занести в таблицу 2.

4. Сравнить периоды колебаний Т для маятников с разной массой шариков m.

Таблица 2

m,кг	№	t, с	tср, с	n	Т, с

5. Проверить зависит ли период колебаний Т математического маятника от длины подвеса ℓ. Для этого по формуле 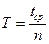, где t_ср (из таблицы 3) среднее значение времени 30 колебаний трех последовательных опытов для каждого из маятников с разной длинной подвеса ℓ. Результаты занести в таблицу 3.

6. Сравнить периоды колебаний Т для маятников с разной длинной подвеса ℓ.

7. Построить график зависимости периода колебаний от длины подвеса Т=f(ℓ).

Таблица 3

ℓ, м	№	t, с	tср, с	n	Т, с

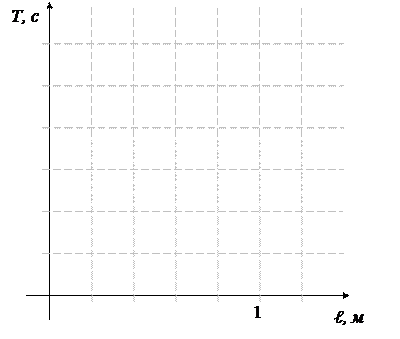Выводы:_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ВОПРОСЫ:

1. Колебательные движения. Гармонические и негармонические колебания. Физические величины, характеризующие гармонические колебания.

2. Закон динамики гармонического колебания в дифференциальной и интегральной форме.

3. Математический маятник. Закон динамики колебательного движения математического маятника. Квазиупругая сила. Период колебания математического маятника.

4. От чего зависит и от чего не зависит период колебания мат. маятника, плоскость колебания? Экспериментальная проверка этих зависимостей?

дата выполнения_____________________________

Преподаватель_____________________________

Дата добавления: 2014-12-27