Изучение колебаний пружинного маятника

ЛАБОРАТОРНАЯ РАБОТА № 6

Оборудование: набор пружин и грузов, секундомер.

Цель работы: исследовать собственные колебания пружинного маятника.

1.Теоретическое введение

Пружинный маятник. Рассмотрим тело массой m, прикрепленное к концу упругой невесомой пружины жесткостью k, другой конец которой закреплен неподвижно (пружинный маятник). Чтобы в уравнение движения тела не вошла сила тяжести, не играющая принципиальной роли для возникновения колебаний, расположим тело на гладкой горизонтальной поверхности, прикрепив свободный конец пружины к неподвижной стенке (рис. 1). Координатную ось Oх направим горизонтально от стенки, выбрав начало отсчета O в центре масс тела, когда оно находится в положении равновесия и пружина не деформирована. Если вывести тело из положения равновесия, сместив его или сообщив ему начальную скорость вдоль оси Oх (или сделав и то, и другое), а затем предоставить самому себе, то оно будет двигаться вдоль этой оси.

Для нахождения кинематического закона движения тела x(t) необходимо записать уравнение движения, т.е. второй закон Ньютона в дифференциальной форме в проекции на ось Oх и найти его решение. Из трех сил, действующих на тело, когда оно находится в некоторой точке траектории с координатой х: силы тяжести 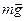, силы реакции опоры 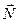и упругой силы 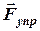- только упругая сила имеет проекцию на ось Oх: F_x = - kx и уравнение движения имеет вид:

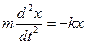. (1)

В математике принято записывать дифференциальное уравнение, располагая функцию и ее производные в левой части уравнения, начиная с производной наивысшего порядка с коэффициентом 1 при ней. В соответствии с этим уравнение (1) перепишем в виде:

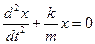. (2)

Вид уравнений (1) и (2) подсказывает искать решение в виде гармонического колебания:

х(t) = Asin(w₀t + j), (3)

так как вторая производная синуса равна самой функции с обратным знаком. О конкретных значениях постоянных величин – амплитуды А, круговой частоты w₀ и начальной фазы j в формуле (3) пока не делается никаких предположений. Действительно ли функция (3) удовлетворяет уравнению (2) и если да, то при каких значениях постоянных А, w₀, j, покажет проверка. Беря вторую производную функции x(t) из (3) по времени: 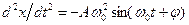и подставляя ее и саму функцию x(t) в уравнение движения (2) имеем:

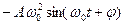+(k/m) 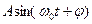= 0.

Сокращая множитель Аsin(w₀t+j), приходим к соотношению 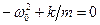, откуда

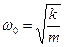. (4)

Таким образом решением уравнения движения (2) является гармоническое колебание с произвольными значениями амплитуды и начальной фазы (множитель Аsin(w₀t+j), в который они входят, в процессе подстановки сократился), но с вполне определенной круговой частотой, определяемой формулой (4). Наличие в решении (3) двух произвольных постоянных А и j гарантирует, что это решение – общее и других решений уравнения движения (2) нет. Чтобы знать, с какими амплитудой и начальной фазой будет происходить колебание, необходима дополнительная информация, например, задание начальных условий – значение координаты и скорости в момент времени t = 0: х(0) = х₀ и u_х(0) = u₀. Потребовав выполнение начальных условий, т.е. приравнивая значения координаты х(t) из (3) и скорости u_x(t) из u_х = Аwsin(wt + p/2) =u_х0 sin(wt + p/2),взятые в момент t = 0, их заданным начальным значениям х₀ и u₀, имеем:

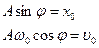(5)

Из этой системы уравнений находим:

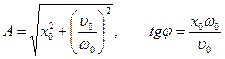. (6)

Рассмотренная задача – типичный пример свободных гармонических колебаний с одной степенью свободы, т.е. описываемых одной изменяющейся со временем координатой, в нашем примере – координатой тела х(t). Их отличительная черта состоит в том, что они всегда происходят с определенной частотой, зависящей только от параметров системы, в нашем случае – от массы тела и жесткости пружины. Что касается амплитуды и фазы, то они определяются начальными условиями, т.е. зависят от способа возбуждения колебаний.

Проведенный анализ показал, что тело совершает гармоническое колебание, если уравнение движения тела имеет вид (1) или, что то же самое (2). Но вид этого уравнения движения предопределен видом выражения для результирующей силы

F_x = - kx. (7)

Причем вовсе не обязательно, чтобы эта сила была упругой, как в случае пружинного маятника; необходимо лишь, чтобы она была направлена к положению равновесия и пропорциональна смещению относительно него. Сила, определяемая формулой (7), независимо от ее физической природы называется квазиупругой. Таким образом, свободные гармонические колебания происходят под действием квазиупругой силы. Если пружинный маятник подвешен вертикально (рис. 2), за счет силы тяжести 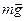положение равновесия сместится вниз на расстояние Dℓ₀ = mg/k, т.к. в положении равновесия сила тяжести уравновешена силой натяжения пружины: kDℓ₀ = mg. В системе координат с началом отсчета в новом положении равновесия 0 уравнение движения имеет вид: m(d²x/dt²) = -k(x+Dℓ₀) + mg, т.к. в этой СО удлинение пружины Dℓ = х +Dℓ₀. Слагаемые -kDℓ₀ и mg в правой части взаимно уничтожаются и уравнение движения принимает обычный вид (1). Следовательно, постоянная сила, действующая наряду с квазиупругой, приводит лишь к смещению положения равновесия, ничего не меняя в характере колебаний.

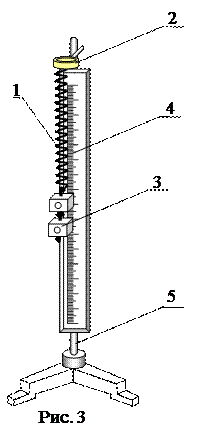
2.Описание лабораторной установки и метода измерения

Пружинный маятник состоит из цилиндрической спиральной пружины 1, закрепленная на держателе 2. На пружину подвешиваются грузы 3 массой m. Амплитуда колебаний груза измеряется по вертикальной шкале 4. Вся система установлена на штативе 5.

3.Порядок выполнения работы и обработка результатов

1. Определите коэффициент жесткости пружины статическим методом. Для этого:

а) подвесьте к пружине один грузик, измерив по шкале удлинение пружины Dℓ;

б) повторите опыт еще два раза, довешивая каждый раз по одному грузику, измеряя при это удлинение пружины Dℓ;

в) зная удлинение пружины Dℓ и массу добавочного груза Dm, вычислить коэффициент жесткости пружины по формуле: 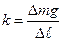при каждом последовательном удлинении;

г) вычислить среднее значение k для каждой из трех пружин. Заполнить таблицу 1;

Таблица 1.

Пружина 1	Dm, кг	Dℓ, м	k, Н/м	Пружина 2	Dm, кг	Dℓ, м	k, Н/м	Пружина 3	Dm, кг	Dℓ, м	k, Н/м
k1ср =	k2ср =	k3ср =

2. Определите период собственных колебаний пружинного маятника. Для этого:

а) выберите пружину 1 и установите на нее один грузик;

б) оттяните грузик на 3 – 4 см вниз и измерьте секундомером время t, в течение которого маятник совершит 10 полных колебаний;

г) измерения повторить не менее трех раз и по ним вычислить среднее значение времени t_ср 10 колебаний для каждой из трех пружин;

д) период собственных колебаний определите из соотношения Т_ср = t_ср/n;

е) опыт повторить для оставшихся пружин. Заполнить таблицу 2.

Таблица 2.

№

Пружина 1

t,с

tср,с

n

Пружина 2

t,с

tср,с

n

Пружина 3

t,с

tср,с

n

Т1ср =

Т2ср =

Т3ср =

3. Определите зависимость периода собственных колебаний пружинного маятника от массы груза. Для этого:

а) выберите одну из пружин и установите один грузик;

б) оттяните грузик на 3 – 4 см вниз и измерьте секундомером время t, в течение которого маятник совершит 10 полных колебаний;

г) измерения повторить не менее трех раз и по ним вычислить среднее значение времени t_ср 10 колебаний;

д) период собственных колебаний определите из соотношения Т_ср = t_ср/n;

е) опыт повторить каждый раз изменяя массу груза на 0.1кг. Заполнить таблицу 3. Построить график зависимости Т от m (Т=f(m)).

Таблица 3.

№	m,кг	t, с	tср, с	n	Т,с	k,Н/м
	0,1					Значения взять из таблицы 1
	0,2
	0,3

4. Определите зависимость периода собственных колебаний пружинного маятника от коэффициента упругости пружины. Для этого:

а) выберите пружину 1 и установите на нее два грузика;

б) оттяните грузики на 3 – 4 см вниз и измерьте секундомером время t, в течение которого маятник совершит 10 полных колебаний;

г) измерения повторить не менее трех раз и по ним вычислить среднее значение времени t_ср 10 колебаний;

д) период собственных колебаний определите из соотношения Т_ср = t_ср/n;

е) опыт повторить для пружин 2 и 3. Заполнить таблицу 4 и построить график зависимости Т от k (Т=f(k)).

Таблица 4.

	№	t, с	tср, с	n	Т,с	k,Н/м
Пружина 1						из таблицы 1
Пружина 2						из таблицы 1
Пружина 3						из таблицы 1

Выводы:__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ВОПРОСЫ:

1. Какое движение называется колебательным? Гармоническим колебанием? Что называется амплитудой, периодом, фазой, частотой?

2. Что называется деформацией? Упругой деформацией? Упругой силой?

3. Закон динамики гармонического колебательного движения в дифференциальной и интегральной форме. Коэффициент возвращающей силы.

4. Потенциальная энергия упруго деформированной пружины.

5. Пружинный маятник. Потенциальная и кинетическая энергии пружинного маятника. Закон сохранения и превращения энергии. Период колебания пружинного маятника.

6. Затухающие колебания. Закон динамики затухающих колебаний в дифференциальной и интегральной формах. Декремент затухания. Логарифмический декремент затухания. Методика их экспериментального определения.

7. Вынужденные колебания. Закон динамики вынужденных колебаний в дифференциальной и интегральной формах. Резонанс.

8. Методика определения коэффициента жесткости пружины.

9. От чего и как зависит период колебаний пружинного маятника?

Для расчетов

дата выполнения_____________________________

Преподаватель_____________________________

Литература:

1. Архангельский М.М. Курс физики. Механика. - М.: Просвещение, 1975.

2. Савельев И.В. Курс общей физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1986.

3. Г.А. Зисман, О.М. Тодес. Курс общей физики. Т.1. Механика, молекулярная физика, колебания и волны. – М.: Наука, 1964.

4. А.С. Шубин. Курс общей физики. - М.: Высш. Школа, 1976.

Содержание

Числовая обработка результатов лабораторного эксперимента.. 3

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ лаб.№1. 5

ИЗМЕРЕНИЕ СКОРОСТИ ПУЛИ МЕТОДОМ БАЛЛИСТИЧЕСКОГО МАЯТНИКА лаб.№2. 11

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ твердого тела лаб.№3. 14

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА лаб.№4. 19

ИЗУЧЕНИЕ гармонических линейных КОЛЕБАНИЙ мат. МАЯТНИКа лаб.№5. 23

ИЗУЧЕНИЕ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА лаб.№6. 28

Литература.. 34

36,1

,2,35

,34,3

,4,33

,32,5

,6,31

,30,7

,8,29

,28,9

10,27

,26,11

,12,25

,24,13

,14,23

,22,15

,16,21

,20,17,

18,19

Дата добавления: 2014-12-27