Аксиомы теории вероятностей. Аксиоматическое определение вероятности

Классическое определение вероятности

Определение вероятности

Вероятность является одним из основных понятий теории вероятностей. Существует несколько определений этого понятия. Одно из основных – это классическое определение. Это определение применимо в случаях, когда удается выделить полную группу несовместных и равновероятных событий, т.е. элементарных исходов.

Вероятностью события А называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех элементарных исходов:

.

(4.1)

Примеры непосредственного вычисления вероятностей.

Пример 5.

В группе 25 студентов. Из них 10 девушек и 15 юношей. Наугад выбирают одного студента. Найти вероятность того, что выберут юношу.

Решение. Искомая вероятность: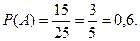

Пример 6.

В группе 15 студентов. Из них 5 девушек и 10 юношей. Выбирают 3 студентов. Найти вероятность того, что из трёх выбранных студентов выберут одну девушку и двух юношей.

Решение. При вычислении вероятности события необходимо обратиться к разделу комбинаторики. Для данной задачи следует подсчитать различные сочетания по формуле (3.3).

Искомая вероятность:

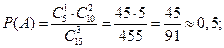
где:

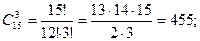
Классическое определение вероятности служит хорошей математической моделью тех случайных экспериментов, число исходов которых конечно, а сами исходы равновозможны и несовместны.

Систему аксиоматического обоснования определения вероятности построил А.Н. Колмогоров в 1933 г.

Числовая функция Р(А), заданная на алгебре F – подмножеств пространства элементарных исходов – W, называется вероятностью случайного события А, если она удовлетворяет следующим свойствам (аксиомам):

А1 (аксиома 1). Р(а) > 0; " A Î F.

Аксиому 1 можно прочитать: «вероятность случайного события А всегда величина положительная для любого события, принадлежащего подмножеству F.

A2 (аксиома 2). P(W)=1.

Аксиома 2 может быть сформулирована следующим образом: вероятность достоверного события равна единице.

A3 (аксиома 3). Если AÇB=Æ то P(AÈB)=P(A)+P(B).

Аксиома 3 может быть сформулирована следующим образом: если события А и В несовместны, то Р(А+В) = P(A)+P(B).

Как следствие из этих аксиом можно сформулировать далее:

Аксиома 4. Вероятность случайного события есть положительное значение, заключенное между нулем и единицей. 0 < Р(А) <1.

Аксиома 5. Вероятность невозможного события равна нулю. Р(А)=0.

Дата добавления: 2014-12-27