Сочетания

Если в выборках из n объектов по m объектов порядок их следования по условию задачи не имеет значения, то размещения, отличающиеся лишь порядком следования, становятся одинаковыми.

Определение 3: Сочетанием называют комбинации, составленные из n различных элементов по m элементов, которые отличаются только составом элементов и не зависят от порядка следования.

.

(3.3)

Сочетания используются, если важен только состав элементов в выборке.

Пример 5.

Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой партой. Порядок их размещения не имеет значения. Определить количество возможных вариантов сочетаний.

Решение.

Количество возможных вариантов сочетаний вычисляется по формуле (3.3):

.

Пример 6.

Флаг государства может комбинироваться из трёх полос разного цвета. Определить число комбинаций из пяти разных цветов, которые можно получить, выбирая из них три полосы разного цвета.

Решение.

Если учитывать порядок в комбинации, то: .

Если же порядок в комбинации не имеет значения, то разных комбинаций:

.

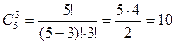3.4. Вопросы для самоконтроля по теме «Комбинаторика»

1. Количество перестановок букв в слове «WORD» равно:

a) 20; b) 24; c) 16; d) 8.

2. Количество перестановок букв в слове «число» равно:

a) 120; b) 24; c) 5; d) 20.

3. Сколько различных трёхбуквенных комбинаций можно составить из букв слова «студент», если все буквы в комбинации различны?

a) 210; b) 240; c) 148; d) 32.

4. Сколько различных комбинаций можно составить из букв слова «победа», если все буквы в комбинации различны?

a) 30; b) 720; c) 120; d) 360.

5. Сколько различных трёхбуквенных комбинаций можно составить из букв слова «победа», если все буквы в комбинации различны?

a) 720; b) 360; c) 120; d) 30.

6. Количество перестановок букв в слове «TIME» равно:

a) 44; b) 26; c) 2; d) 24.

7. Сколько различных чисел можно составить из пяти цифр: 9, 7, 8, 1, 6, если все цифры в числе разные?

a) 120; b) 60; c) 24; d) 0.

8. Сколько различных двузначных чисел можно составить из пяти цифр: 5, 7, 8, 4, 1, если все цифры в числе разные?

a) 24; b) 20; c) 120; d) 60.

9. Сколько различных трёхзначных чисел можно составить из шести цифр: 1, 2, 3, 4, 5, 6, если все цифры в числе различны?

a) 360; b) 120; c) 60; d) 240.

10. Сколько различных трёхбуквенных комбинаций можно составить из букв слова «ГРОМ», если все буквы в комбинации различны?

a) 6; b) 24; c) 4; d) 12.

11. Сколько различных двухбуквенных комбинаций можно составить из букв слова «ЗАЧЁТ», если все буквы в комбинации различны?

a) 4; b) 120; c) 60; d) 20.

12. Сколько различных трёхзначных чисел можно составить из пяти цифр: 7, 5, 3, 4,1, если все цифры в числе разные?

a) 4; b) 120; c) 60; d) 20.

Дата добавления: 2014-12-27