Размещения. Задачи, связанные с перестановками, относятся к задачам комбинаторики

Перестановки

Задачи, связанные с перестановками, относятся к задачам комбинаторики. Например, перестановка книг на полках. В таких задачах подсчитывается количество возможных вариантов перестановок, причем в каждой комбинации должны присутствовать все объекты строго по одному разу.

Определение 1: Перестановками называют комбинации, состоящие из одних и тех же n – различных элементов и отличающиеся только порядком их расположения.

Рn = n! = 1× 2× 3× …× n.

(3.1)

где: Р_n – количество перестановок;

n! = 1 · 2 · 3· … · (n - 1) · n – произведение всех натуральных чисел от 1 до n включительно есть «n-факториал».

Необходимо учитывать, что факториал нуля равен единице: 0! = 1.

Пример 1.

Определить количество трехзначных чисел, которые можно составить из трех цифр: 3, 5, 7, с учётом использования каждой цифры в числе строго по одному разу.

Решение.

Количество трехзначных чисел в данном примере определяется по формуле перестановок (3.1) и равно: Р₃= 1× 2× 3=6.

Пример 2.

Подсчитать количество способов расстановки на полке 5 разных книг.

Решение.

На первое место можно поставить любую из 5 книг, для каждого варианта первой книги на второе место может быть поставлена любая из оставшихся 4 книг. Итак, число перестановок из 5 книг равно:

5! = 5×4×3×2×1= 120.

Если в выборках из n объектов по m объектов порядок их следования по условию задачи имеет значения, то имеют дело с «задачей о рассаживании»: группу из n человек следует рассадить в аудитории за каждым столом по m-человек (m<n). Число способов рассаживания определяется числом размещений.

Определение 2: Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком следования.

.

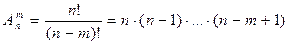(3.2)

Пример 3.

Группу из 20 студентов можно разместить в аудитории по 2 человека за каждой партой. Порядок их размещения имеет значение.

Решение.

Количество возможных вариантов размещений вычисляется по формуле (3.2):

.

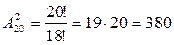Пример 4.

Найти количество трехзначных чисел с неповторяющимися цифрами, которые можно составить из цифр: 1, 2, 3, 4, 5.

Решение.

Количество трехзначных чисел в данном примере определяется по формуле размещений (3.2) и равно: .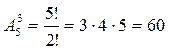

Дата добавления: 2014-12-27