Рациональные и дробно-рациональные уравнения

Определение 4.7. Функция вида , где 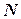; - некоторые действительные числа, называется целой рациональной функцией.

Определение 4.8. Целым рациональным уравнением называется уравнение вида , где - целая рациональная функция.

Пример 4.10. Решить уравнение .

Решение.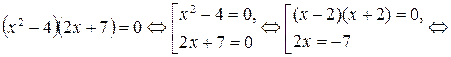

Ответ: .

Пример 4.11. Решить уравнение .

Решение. Данное уравнение называют биквадратным. С помощью замены , , оно может быть сведено к решению квадратного уравнения.

Выполняя указанную выше замену, получаем

Делая обратную подстановку, окончательно имеем

Ответ: ; .

Пример 4.12. Решить уравнение .

Решение. Так как коэффициенты уравнения – целые числа, то попробуем подобрать хотя бы один целый корень. Делителями свободного члена являются числа . Подставляя их в уравнение, убеждаемся, что - корень уравнения.

Проведем деление многочленов:

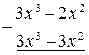
Тогда .

Аналогично, убеждаемся, что также является корнем многочлена , проведем деление:

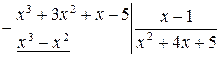
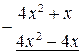
Таким образом, исходное уравнение можно записать в виде:

Дискриминант второго уравнения 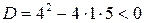, следовательно, оно не имеет действительных корней. Таким образом, решением исходного уравнения является .

Ответ: .

Определение 4.9. Дробно-рациональным уравнением называется уравнение вида , где 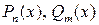- многочлены.

Решение дробно-рационального уравнения сводится к решению уравнения и проверке того, что найденные корни удовлетворяют условию , то есть дробно-рациональное уравнение равносильно системе:

Пример 4.13. Решить уравнение .

Решение. Найдем предварительно область определения заданного уравнения:

.

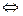
Далее все преобразования будем проводить на области определения уравнения. Умножим обе части уравнения на , тогда имеем

.

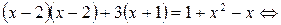
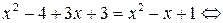
Ответ: .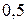

Пример 4.14. Решить уравнение .

Решение. Область определения уравнения имеет вид:

.

Далее будем проводить решение на области определения уравнения. Так как ; , то естественно сделать замену . Тогда исходное уравнение примет вид:

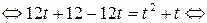
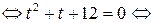
Делая обратную замену, получаем

.

Ответ: ; .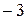

Пример 4.15. Решить уравнение .

Решение. Непосредственно подстановкой устанавливаем, что не является решением исходного уравнения. Вынесем из каждой скобки:

.

Делая замену , получаем

Проведем обратную подстановку, тогда

Ответ: ; .

Пример 4.16. Решить уравнение .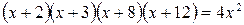

Решение. Проведем группировку множителей в левой части уравнения так, чтобы при перемножении были равны первый коэффициент и свободный член:

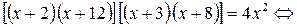
Далее проведем процедуру аналогично примеру 4.15. Так как не является корнем уравнения, вынесем его за скобки:

.

Сделаем замену: , тогда

или, делая обратную замену, окончательно получаем

.

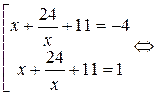
Ответ: .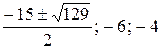

Пример 4.17. Решить уравнение .

Решение. Так как не является решением уравнения, разделим обе части уравнения на , тогда получим:

.

Сделаем замену , тогда

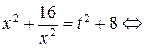
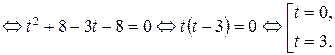
Переходя обратно к переменным , имеем

.

Ответ: .

Дата добавления: 2014-12-27