Рациональные и дробно-рациональные неравенства. Метод интервалов для рациональных неравенств

Квадратные неравенства

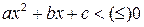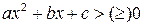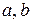Определение 5.5. Квадратными неравенствами называются неравенства вида , , где и 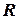, - переменная, при этом .

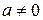Выделяют два основных метода решения квадратных неравенств – графический и аналитический.

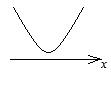
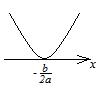
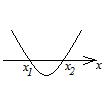
1. Графический метод. Решение определяется в зависимости от расположения графика (таблица 5.1).

Таблица 5.1.

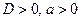
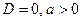
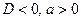
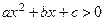
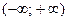
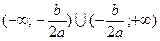
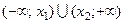
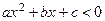
	нет решений	нет решений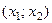
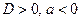
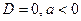
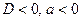
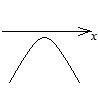
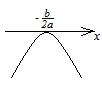
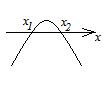
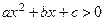
	нет решений	нет решений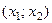

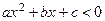
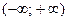
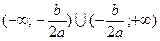
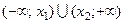
2. Аналитический метод. Если 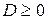, то квадратный трехчлен раскладывают на множители и полученное равносильное неравенство решают методом интервалов (см. пункт 5.3).

Важнейшим методом решения неравенств является метод интервалов. Данный метод основан на том, что двучлен 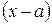положителен при 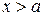и отрицателен при 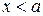, то есть меняет знак при переходе через точку .

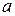Кроме того полезно использовать следующие правила:

1. двучлен 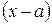в нечетной степени ведет себя так же, как ;

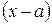2. двучлен 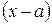в четной степени не меняет знак при переходе через точку ;

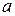3. квадратный трехчлен 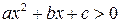при 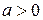, , 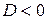поэтому он может быть опущен при решении любого неравенства;

4. при переходе через точку 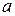может изменить знак только множитель вида 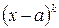, а выражени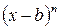е , где 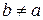, при переходе через точку 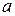знак не меняет.

Пример 5.1. Решить неравенство .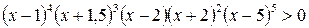

Решение. Для решения строгого неравенства наносим на числовую ось нули функции кружочками («дырками»). Далее расставляем знаки, используя приведенные выше правила:

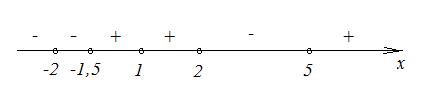
Тогда решение неравенства имеет вид: .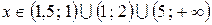

Ответ: .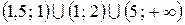

Пример 5.2. Решить неравенство .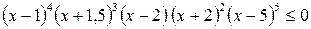

Решение. Напомним, что по определению,

.

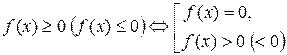Для решения нестрогих неравенств наносим нули функции на числовую ось точками. Затем расставляем знаки в промежутках:

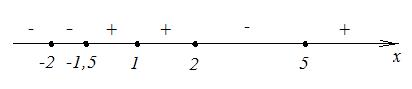
Решение примет вид: .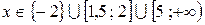

Ответ: .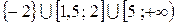

Определение 5.6. Неравенства вида 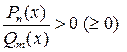, , 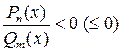где 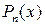, 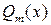- многочлены, называются рациональными.

Для решения рациональных неравенств необходимо предварительно сделать следующие преобразования:

1. все члены неравенства перенести в одну сторону и привести к общему знаменателю;

2. выражения, стоящие в числители и знаменатели разложить на множители;

3. определить нули числителя и знаменателя;

4. применить метод интервалов.

Замечание 5.1. М е тод интервалов применяется к дроби точно так же, как и к многочленам. Для нестрого же неравенства имеем:

.

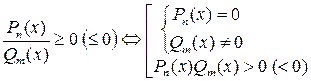При решении нестрогих рациональных неравенств нули числителя наносятся на числовую ось точками, а нули знаменателя (и нули числителя, если они равны нулям знаменателя) - «дырками».

Пример 5.3. Решить неравенство .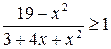

Дата добавления: 2014-12-27