Тобольск – 2011

Учебное пособие

Семинарские и практические занятия

УЧАЩИХСЯ ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЫ

МЕТОДИКА ОБУЧЕНИЯ МАТЕМАТИКЕ

С.В Демисенова, Л.П.Шебанова, З.И.Янсуфина

Решить неравенство (1-9).

Группа С

Решить неравенство (1-10).

Группа B

1. 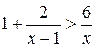. (Ответ: .)

2. 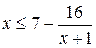. (Ответ: .)

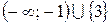3. 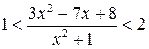. (Ответ: .)

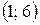4. 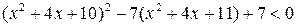. (Ответ: .)

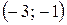5. 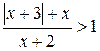. (Ответ: .)

6. 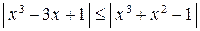. (Ответ: .)

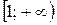7. 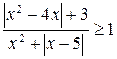. (Ответ: .)

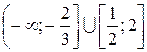8. 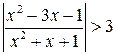. (Ответ: .)

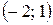9. 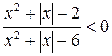. (Ответ: .)

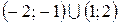10. . (Ответ: .)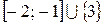

11. 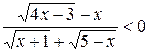. (Ответ: .)

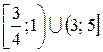12. 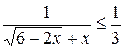. (Ответ: .)

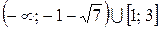13. 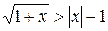. (Ответ: .)

1. 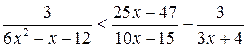. (Ответ: .)

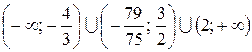2. 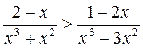. (Ответ: .)

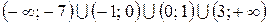3. 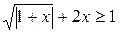. (Ответ: .)

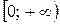4. 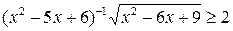. (Ответ: .)

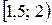5. 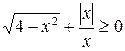. (Ответ: .)

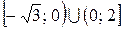6. 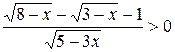. (Ответ: .)

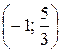7. 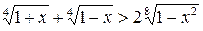. (Ответ: .)

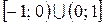8. 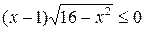. (Ответ: .)

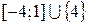9. 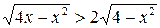. (Ответ: .)

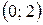УДК 37.022 Печатается по решению

ББК 74.586.221 редакционно-издательского совета

Д 30 ТГПИ им. Д.И. Менделеева

Демисенова С.В., Шебанова Л.П., Янсуфина З.И. Методика обучения математике учащихся общеобразовательной школы: Учебное пособие – Тобольск: ТГСПА им. Д.И.Менделеева, 2011. – 164 с.

Пособие разработано в соответствии с ФГОС ВПО по направлению подготовки «Педагогическое образование», про профилю «Математическое образование» для организации самостоятельной работы студентов по дисциплине «Методика обучения и воспитания (математика)». В пособии сформулированы основные цели и задачи изучения дисциплины, требования к подготовке студентов, приведено примерное тематическое планирование, показана организация учебного процесса, представлены задания для самостоятельной работы. Ко всем видам заданий даны указания для их выполнения, представлены примеры их выполнения; предложен список основной и дополнительной литературы.

Представленные материалы и методические рекомендации могут быть использованы в практике работы преподавателей методики обучения математике, учителей математики и студентов педвузов.

Научный редактор: Заслуженный учитель РФ,

доктор педагогических наук, профессор О.Б.Епишева

Рецензенты:

А.Т. Зверева, канд.пед.наук, доцент, декан факультета математики и информационных технологий Курганского государственного университета.

Т.В. Рублева, канд.пед.наук, доцент кафедры педагогики ТГСПА им. Д.И. Менделеева

ISBN 978-5-85944-2300

© ТГСПА им. Д.И. Менделеева, 2011

© С.В.Демисенова, 2011

© Л.П.Шебанова, 2011

© З.И.Янсуфина, 2011

ПРЕДИСЛОВИЕ

Настоящее учебное пособие включает вопросы общей методики обучения математике, закономерности и особенности изучения материала содержательно-методических линий школьного курса арифметики, алгебры и начал анализа и геометрии, выделенных в федеральном компоненте Государственного стандарта для средней (полной) общеобразовательной школы по образовательной области «Математика».

В данном пособии представлен материал для организации самостоятельной работы студентов при подготовке к практическим и семинарским занятиям. Пособие содержит четыре раздела:

– фрагмент рабочей программы дисциплины «Методика обучения и воспитания (математика)», включающий основные задачи дисциплины; требования к уровню подготовки бакалавров через результаты освоения: знания, умения, навыки, компетенции; тематическое планирование; структуру учебного процесса;

– содержание семинарских и практических занятий: виды учебных заданий с указаниями и примерами их выполнения;

– виды и содержание контроля;

– список рекомендуемой литературы.

Содержание пособия соединяет в себе как традиционные, так и инновационные подходы в обучении будущих преподавателей математики. В современной концепции образования превалирующей является направленность на всестороннее развитие ребенка, и в связи с этим наиболее перспективным для методики обучения математике в настоящее время является личностно-ориентированный подход. В пособии отражены так же технологический, деятельностный, дифференцированный, информационный подходы.

Авторы выражают благодарность рецензентам –

Замечания и предложения по содержанию пособия будут с благодарностью приняты по адресу: 626150, г. Тобольск, ул. Знаменского 58, ауд. 402

Авторы

РАЗДЕЛ I

ФРАГМЕНТ РАБОЧЕЙ ПРОГРАММЫ ДИСЦИПЛИНЫ

«Методика обучения и воспитания (математика)»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Методическая подготовка является системообразующим компонентом всей профессиональной подготовки преподавателя математики. В процессе изучения дисциплины используются инновационные подходы к совершенствованию методической подготовки преподавателя математики в педвузе: личностно-ориентированный, дифференцированный, информационный, деятельностный, технологический, компетентностный, интегративный.

Личностно-ориентированный подход предполагает учет не только возрастных, но и индивидуально-типологических свойств личности, понимание и знание которых будущими преподавателями во многом определят эффективность обучения учащихся. Личностно-ориентированное обучение рассматривается в рамках дифференцированного подхода.

Становление преподавателя математики определяется повышением уровня его образованности. Дифференцированный подходк обучению студентов определяется уровнями усвоения любой единицы информации: 1-й уровень (понял, запомнил, воспроизвел) – минимальный; 2-й уровень (применил усвоенное в стандартной ситуации) – обязательный; 3-й уровень (перенес усвоенное в нестандартную ситуацию) – уровень возможностей; 4-й уровень (решил нестандартную задачу) – творческий. Реализация дифференцированного подхода осуществляется через: 1) проектирование дифференцированных целей обучения; 2) проектирование дифференцированных учебных задач для достижения этих целей; 3) организацию учебного процесса с использованием различных (дифференцированных) форм деятельности по решению учебных задач; 4) организацию дифференцированного контроля и оценки усвоения.

Обновление системы профессионального образования сегодня непосредственно связано с использованием такого мощного средства, как компьютер, для эффективной организации учебно-познавательной деятельности студентов, для управления и организации учебно-воспитательного процесса, а также для подготовки студентов к использованию информационных технологий обучения математике в будущей профессиональной деятельности.

Профессионализм педагога определяется уровнем и способом владения различными видами педагогической деятельности. Поэтому психологической основой совершенствования методической подготовки преподавателя математики является деятельностный подход к обучению с выделением видов деятельности преподавателя и студентов. Деятельностный характер носят: 1) цели обучения (выраженные в действиях студентов), 2) содержание обучения, включающее учебные методические задачи для формирования умений выполнять соответствующие действия по их решению и 3) учебный процесс, основной структурной единицей которого является решение учебных задач.

Описанные выше подходы по существу означают использование в обучении элементов технологического подхода, т.к. технологический подход к обучению означает:

– проектирование дифференцированных целей, выраженных в действиях студента: студент знает …, понимает …, умеет …;

– представление содержания обучения в виде системы дифференцированных по уровням математической и учебно-методической деятельности учебных заданий;

– использование в организации учебного занятия всех видов учебного общения, а также различного сочетания фронтальной, групповой, коллективной и индивидуальной форм учебной деятельности студентов;

– осуществление контроля усвоения знаний и способов деятельности в трех видах: 1) входной контроль – для информации об уровне готовности студентов к работе и, при необходимости, коррекция этого уровня; 2) текущий контроль после изучения каждой темы; 3) итоговый контроль – контрольные работы, зачет, экзамен;

– использование для оценки уровня усвоения знаний и способов деятельности разноуровневых тестовых контрольных работ.

Компетентностный подход в образовании означает ориентацию на результаты любой его ступени, связанные с усилением его практической (деятельностной) составляющей, значимой за его пределами, т.е. не на сумме усвоенной обучаемыми информации, а на способности выпускника учебного заведения адаптироваться и самостоятельно действовать в различных ситуациях, решать проблемы различной сложности на основе имеющихся знаний. Он усиливает практико-ориентированность образования, его предметно-профессиональный аспект, подчеркивает роль опыта, умений практически использовать и реализовать знания, решать задачи.

Интегративный подходк совершенствованию методической подготовки преподавателя математики осуществляется как всесторонняя связь элементарной математики и методики обучения математик.Указанные возможности создаются, прежде всего, при изучении таких стержневых содержательно-методических линий школьного курса математики, как числа и вычисления, тождественные преобразования выражений, уравнения и неравенства, функции, геометрические фигуры и другие вопросы геометрии. Глубокое теоретическое обоснование этих вопросов невозможно только в курсе методики обучения математике, а изучаемые только в курсе элементарной математики, они не имеют необходимой методической «окраски». Интеграция эффективна и при изучении общей методики обучения математике, если при этом содержание курса элементарной математики являются методологические и теоретико-логические основы школьного курса математики. В этом случае целостность курса обеспечивает формирование общематематической и общеметодической культуры преподавателя математики.

Дата добавления: 2014-12-27