Решению арифметической задачи

Методика обучения учащихся

В качестве примера рассмотрим следующую задачу (5 класс): «Велосипедист ехал 3 часа со скоростью 18 км/ч. Обратно он ехал другой дорогой, которая была короче на 9 км, но ехал со скоростью на 3 км/ч меньшей. Сколько времени велосипедист затратил на обратную дорогу?»

1. Подготовительный этап. Изучить содержания задачи - установить зависимости между расстоянием, скоростью и временем; может быть представлено в системе устных упражнений через выполнение заданий на повторение этих зависимостей. Например, задача: «Пешеход идет в течение 3-х часов со скоростью 5 км/ч.» Что можно определить? (расстояние) Как? (можно определить расстояние: () км). Записать зависимость формулой (S = v t, =15).

2. Чтение задачи. Записать содержание задачи (если в задаче встречаются незнакомые термины, выяснить их смысл). Содержание задачи может быть записано по-разному. Например, с помощью таблицы или схемы (рис.3):

Таблица 12

	Скорость	Время	Расстояние
1 путь	18 км/ч	3 ч	?
2 путь (обратный)	На 3 км/ч медленнее	?	на 9 км короче

Скорость на пути АВ – 18 км/ч;

Время движения на АВ – 3 ч;

Расстояние АВ -?

Скорость на пути ВА (?) – на 3 км/ч меньше, чем скорость

Расстояние ВА -? – на 9 км меньше, чем

Время движения на ВА -?

Рис. 3. Изучение содержания задачи (схема)

3. Анализ содержания и составление плана решения задачи. Анализ содержания задачи (поиск решения) может быть представлен:

а) в виде схемы (рис. 4)

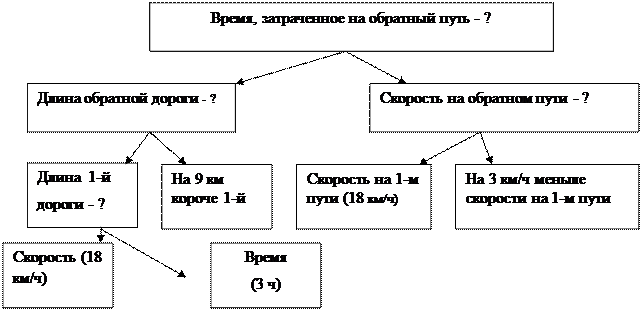
Рис.4. Анализ содержания задачи (схема)

б) системы вопросов:

1) Какой главный вопрос задачи? (Сколько времени велосипедист затратил на обратную дорогу?)

2) Можно ли сразу на него ответить? (Нет, т. к. неизвестны обратный путь и скорость велосипедиста на обратном пути).

3) Нельзя ли определить скорость велосипедиста на обратном пути? (Можно, т. к. известна скорость велосипедиста на 1-м пути, и известно, насколько она отличается от скорости на отрезке пути).

4) Нельзя ли определить длину обратного пути? (Сразу нет, но можно сначала найти длину первого пути, т. к. известна скорость и время, а затем и длину 2-го пути).

План решения задачи:

Найти последовательно:

1) длину 1-го пути;

2) длину 2-го пути;

3) скорость на 2 участке пути;

4) время, затраченное на обратную дорогу;

4. Выполняем план решения задачи (рис.5).

Синтез решения задачи:

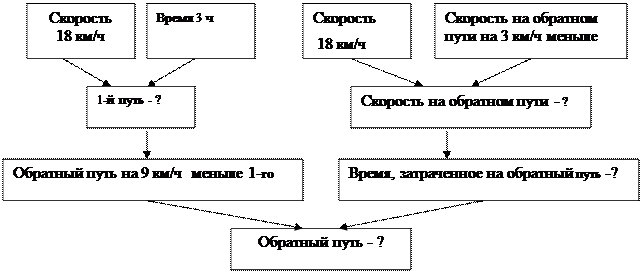Рис.5. Синтез решения задачи (схема)

Способы записи решения задачи

1-й способ

Запись решения числовой формулой

1. На 1-м пути велосипедист проехал: 18 * 3 км.

2. На обратном пути велосипедист проехал: (18 * 3 – 9) км.

3. Скорость велосипедиста на обратном пути: (18 – 3) км/ч.

4. На обратный путь велосипедист затратил: (18 * 3 – 9): (18 – 3) ч.

Находим числовое значение выражения (устно).

Ответ: на обратный путь велосипедист затратил 3 часа.

2-й способ

Вопросно-ответная форма

1. Какова длина первой дороги? 18 * 3 = 54 (км)

2. Какова длина второй дороги? 54 – 9 = 45 (км)

3. Какова скорость велосипедиста на обратном пути? 18 – 3 = 15 (км/ч)

4. Сколько времени затрачено на обратную дорогу? 45: 15 = 3 (ч)

Ответ: 3 часа.

3-й способ

Запись только действий

1. 18 * 3 = 54 (км).

2. 54 – 9 = 45 (км).

3. 18 – 3 = 15 (км/ч).

4. 45: 15 = 3 (ч).

Ответ: 3 часа.

4-й способ

Запись решения с пояснением

1. 18 * 3 = 54 (км) – длина 1-го пути.

2. 54 – 9 = 45 (км) – длина 2-го пути.

3. 18 – 3 = 15 (км/ч) – скорость велосипедиста на 2 участке пути.

4. 45: 15 = 3 (ч) – затратил велосипедист на обратный путь.

Ответ. 3 часа.

Дополнительная работа над задачей после ее решения

1. Запись решения задачи в виде числовой формулы, если запись была иной.

2. Составление задачи, аналогичной решенной.

3. Составление одной из обратных задач и другие способы.

4. Выявление и обобщение действий по решению задачи.

Замечание: Формулировка той же задачи может быть дана иначе. Например: «Коля и Петя ехали из города разными дорогами в лагерь. Коля ехал по дороге, которая была короче на 9 км, но ехал со скоростью на 3 км/ч меньшей, чем Петя. А Петя ехал 3 часа со скоростью 18 км/ч». Поставьте вопрос и решите задачу (Кто из мальчиков раньше приедет в лагерь?).

Дата добавления: 2014-12-27