Закон сообщающихся сосудов

Основное уравнение гидростатики.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМАМ

«СТАТИКА, ДИНАМИКА, ОДНОМЕРНЫЕ ПОТОКИ ЖИДКОСТИ»

Задача 1

На поршень одного из сообщающихся сосудов, наполненных водой, действует сила P₁ = 20 кГ, а на поршень второго сосуда – Р₂ = 30 кГ. Определить разность уровней жидкости в сосудах h, если диаметр первого поршня d₁ = 0,1 м, второго поршня d₂ = 0,15 м (рис. 1).

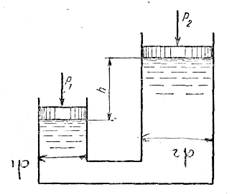
Рис. 1

Дано: Р₁ = 20 кГ, Р₂ = 30 кГ, d₁ = 0,10 м, d₂ = 0,15 м.

Определить: h.

Решение

Давление на единицу площади на поверхности жидкости под первым поршнем:

.

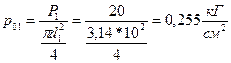То же на поверхности жидкости под вторым поршнем:

.

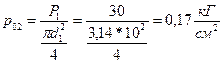Гидростатическое давление во втором сосуде на глубине h определяется по основному уравнению гидростатики: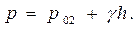

Так как жидкость находится в покое, то можно записать: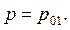

Тогда: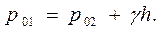

Откуда: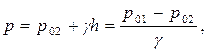

где объемный вес воды g = 1 Г/см³ = 0,001 кГ/см³.

Задача 2

В замкнутом сосуде с водой абсолютное давление на свободной поверхности равно р_о = 2,85 кГ/см². На какую высоту Н поднимется вода в открытой трубе, сообщающейся с сосудом на глубине h (м) под свободной поверхностью (рис. 2)?

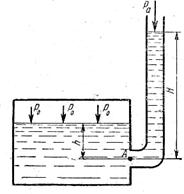
Рис. 2

Дано: р₀ = 2,85 кГ/см², h = 1,4 м = 140 см.

Определить: H.

Решение

По условию задачи нам требуется определить, на какую высоту поднимется вода в открытой тонкой трубке, сообщающейся с сосудом; а это есть не что иное, как пьезометрическая высота, которая может быть определена по формуле: ,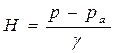

где р – абсолютное давление внутри сосуда в точке А;

р_а – атмосферное давление, действующее на воду со стороны открытой части трубки;

p – p_a = p_из, то есть избыточное давление;

g – объемный вес воды.

Зная, что p = p₀ +gh и объемный вес воды g = 0,001 кГ/см³, а атмосферное давление р_а = 1,033 кГ/см², можем написать:

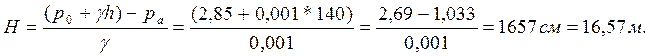
3адача 3

Требуется определить подъемное усилие Т для подъема в канале прямоугольного щита, с двух сторон которого находится вода. Щит может вращаться вокруг горизонтальной оси m. Задачу следует решить аналитически, построить эпюры давления и найти центры давления для сил суммарных гидростатических давлений. На чертеже показать все силы давления и вес щита, а также координаты точек их приложения (рис. 3 и рис. 3а).

Дано: H₁ = 7,2 м, Н₂ = 3,15 м,

,

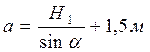угол наклона a = 60°, ширина щита b = 4 м, вес щита G = 3,25 Т. Трением в шарнире можно пренебречь.

Определить: Т.

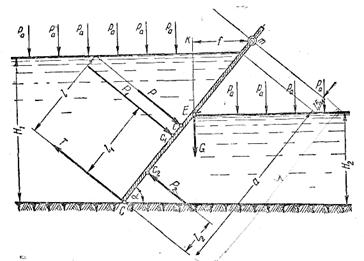
Рис. 3

Решение

Из теоремы моментов мы знаем, что алгебраическая сумма моментов всех действующих сил относительно какой-либо точки равна нулю; поэтому можем написать следующее уравнение в общем виде:

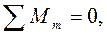
или в нашем случае:

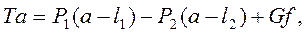
где точкой моментов является точка «m» на оси вращения.

Найдя числовые значения для Р₁, Р₂, l₁, l₂ G, f, сможем определить величину подъемного усилия Т.

Длину щита можно вычислить по заданной в задаче формуле, зная, что a = 60° и Н₁ = 7,2 м,

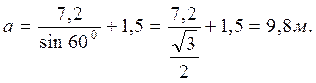
Силу гидростатического давления воды слева от щита P₁ определим по следующей формуле (для наклонной плоскости):

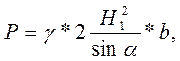
где ширина щита b = 4 м,

объемный вес воды g = 1 Т/м³,

высота столба воды слева от щита H₁ = 7,2 м, a = 60°.

Тогда:

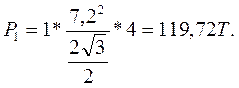
Сила Р₂ справа от щита:

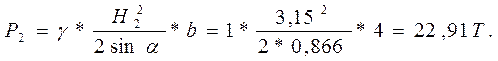
Равнодействующая сил гидростатического давления Р будет:

P = P₁ – P₂ = 119,72 – 22,91 = 96,81 Т.

Величины l₁ и l₂, то есть расстояние от низа стенки до центра давления соответствующей силы гидростатического давления воды на щит, определим по следующим формулам:

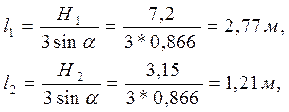
Плечо силы G может быть определено из уравнения:

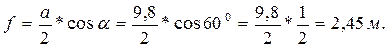
Зная теперь все необходимые величины, можно вычислить величину подъемного усилия Т:

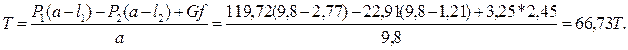
Построим теперь эпюры гидростатического давления воды для сил давления воды на щит слева и справа, а также и для их равнодействующей сил, определив графически и аналитически ее центр давления (рис. 3а).

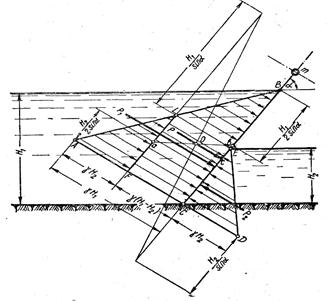
Рис. 3а

SD ABC выражает собой величину силы гидростатического давления воды Р₁ действующей на щит слева;

SD ДСЕ выражает собой величину силы гидростатического давления воды Р₂, действующей на щит справа;

S трапеции CFLB выражает собой величину равнодействующей силы Р.

Для графического определения точки с, то есть центра давления равнодействующей силы давления воды на щит, находим в начале центр тяжести трапеции, то есть точку О и из нее опускаем перпендикуляр на щит; точка пересечения перпендикуляра со щитом и будет центром давления.

Центр давления равнодействующей силы давления воды на щит можно найти и аналитически. Для этого напишем, пользуясь теоремой Вариньона, уравнение моментов равнодействующей и составляющих ее гидростатических сил относительно точки С (рис. 3):

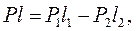
Откуда:

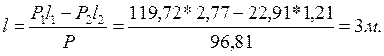
Ординаты эпюр гидростатического давления, как известно, выражают собой гидростатические напряжения в соответствующих точках щита или стенки, а их площади – силы гидростатического давления воды.

Задача 4

Донное отверстие плотины перекрывается плоским прямоугольным щитом, шарнирно прикрепленным к телу плотины своей верхней кромкой. Определить, какое усилие нужно приложить к тросу для открытия щита при следующих данных: глубина погружения нижней кромки щита H = 3 м, высота щита h = 1 м, ширина щита b = 1,5 м, угол между направлением троса и горизонтом a = 45° (рис. 4).

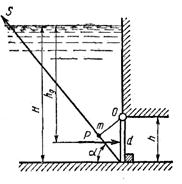
Рис. 4

Дано: H = 3 м, h = 1,0 м, b = 1,5 ж, a = 45°.

Определить: S.

Решение

Давление воды Р на щит определяем по формуле:

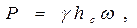
где площадь щита

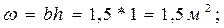
глубина погружения центра тяжести щита

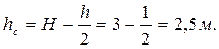
Стало быть,

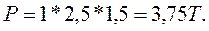
Глубину погружения центра давления щита находим по формуле:

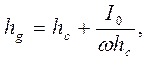
где центральный момент инерции площади щита:

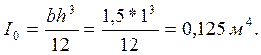
Тогда

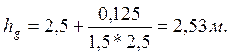
Усилие для открытия щита определяется из равенства моментов:

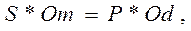
откуда

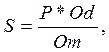
где

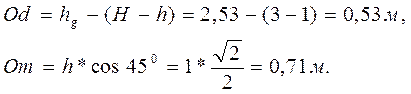
Поэтому

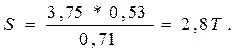
Задача 5

Определить давление на стенки и сферическое дно вертикального цилиндрического резервуара, сваренного из пяти поясов листовой стали при высоте каждого пояса h, и рассчитать толщину стенок, если резервуар наполнен водой доверху. Кроме того, начертить эпюры давления на стенки и дно резервуара и графически найти центры дав­ления (рис. 5).

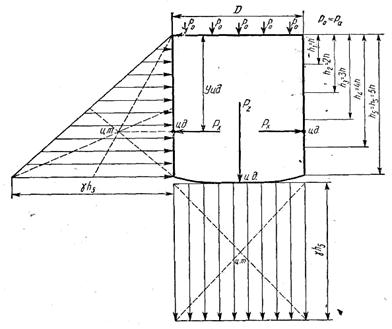
Рис. 5

Дано: внутренний диаметр резервуара D = 9 м, допускаемое напряжение стали на разрыв s_z = 1400 кГ/см², h = 1,9 м.

Определить: Р_х, P_z, d_i.

Решение

Давление на стенки вертикального цилиндрического резервуара можно определить по формуле:

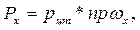
где 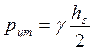, но так как h_s = 5h,

то

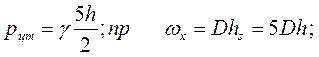
поэтому окончательно для Р_х получим:

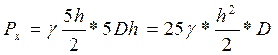
или

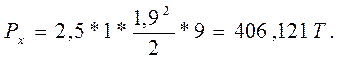
Давление на дно резервуара (очертанием кривизны дна резервуара пренебрегаем) может быть определено по следующей формуле:

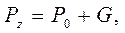
но Р₀ = Р_а, где Р_а – сила, обусловленная атмосферным давлением, действует изнутри и снаружи резервуара, взаимно уравновешивается и в расчет не принимается.

Тогда

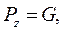
где G – вес жидкости в резервуаре, то есть

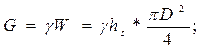
но так как

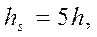
то

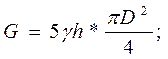
поэтому

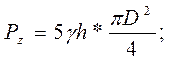
или

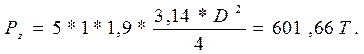
Толщину стенки вертикального резервуара будем определять по формуле:

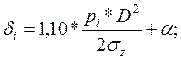
где 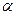= 2…5 мм – запас на коррозию, 1,10 – запас на сварные швы.

Сначала определим р для каждого пояса, отнеся его к центру тяжести пояса, по формуле:

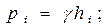
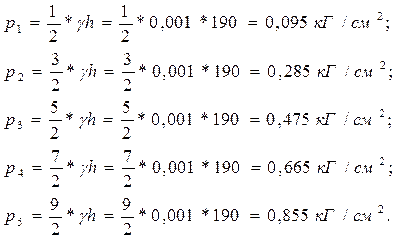
Зная величины р, найдем теперь толщину стенки резервуара в каждом его поясе:

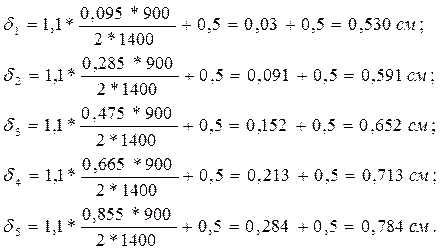
Полученные размеры толщин листов округляем до стандартных размеров, обеспечивая запас жесткости, и принимаем: для четырех верхних поясов вертикального цилиндрического резервуара прокатный лист толщиной 8 мм; для нижнего пояса вертикального цилиндрического резервуара прокатный лист толщиной 10 мм.

Задача 6

Сферическая крышка, закрывающая круглое отверстие в стенке резервуара, прикреплена к нему двумя болтами (рис. 6). Определить растягивающие усилия, возникающие в каждом из болтов а и b, если глубина погружения центра отверстия h_c = 2 м и диаметр крышки d = 1,0 м.

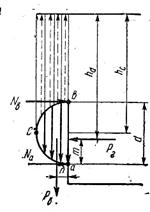
Рис. 6

Дано: h_c = 2 м, d= 1,0 м.

Определить: N_a и N_B.

Решение

Горизонтальная составляющая равнодействующей давления воды на крышку:

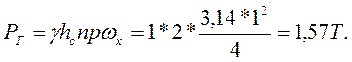
Вертикальная составляющая давления воды на крышку:

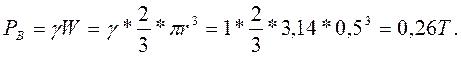
При построении тела давления криволинейная поверхность крышки аb разделяется на две части ас и cb. Тело давления асеf для нижней части крышки действует сверху вниз; тело давления bсef для верхней части крышки действует снизу вверх. Общий объем тела дав­ления для крышки определится как разность объемов тел давления для нижней и верхней части крышки и будет равен объему полусферы диаметром d. Общий объем тела давления заштрихован на рисунке сплошными жирными линиями.

Растягивающие усилия, возникающие в болтах, найдем из уравнений равновесия крышки:

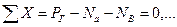(1) (1)

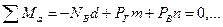(2)

где т – расстояние от точки а до линии действия горизонтальной составляющей давления воды на крышку:

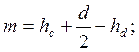
глубина погружения центра давления

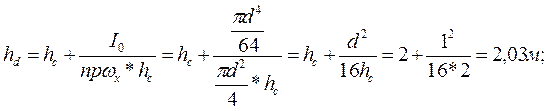
поэтому

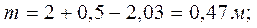
n – расстояние от точки а до линии действия вертикальной составляющей гидростатического давления воды на крышку. Из геометрии известно, что для полушара:

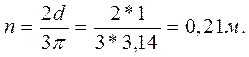
Из уравнения равновесия крышки (2) имеем:

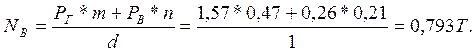
Из уравнения равновесия (1):

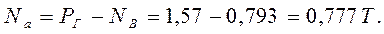
Дата добавления: 2014-12-27