Аналитическое отделение корней

Графическое отделение корней

Графическое отделение корнейосновано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.

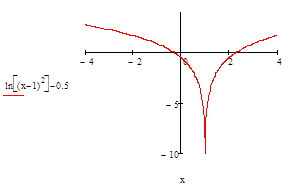
Пример 6.2.2-1. Отделить корни уравнения ln (x-1)² – 0.5 = 0.

На рис. 6.2.2-1 изображен график функции y = ln (x-1)² – 0.5, из которого следует, что уравнение имеет два действительных корня 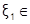[-1;0] и 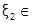[2;3].

Рис.6.2.2-1

В некоторых случаях удобно вначале преобразовать функцию f(x) к виду f(x)=g₁(x ) - g₂(x), из которого, при условии f(x)=0, следует, что g₁(x)=g₂(x). При построении графиков y₁=g₁(x ) и y₂=g₂(x)находят отрезки, содержащие точки пересечения этих графиков.

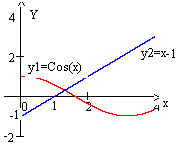
Пример 6.2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.

Приведем исходное уравнение к виду сos(x)= x – 1. Построив графики функций y₁ = сos(x) и y₂ = х – 1 (рис. 6.2.2), выделим отрезок, содержащий корень 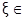[1;2].

Рис. 6.2.2-2

Аналитическое отделение корней основано на следующей теореме.

Если функция f(x ) непрерывна и монотонна на отрезке [a;b] и принимает на концах отрезка значения разных знаков, то на отрезке [a;b] содержится один корень уравнения f(x)=0.

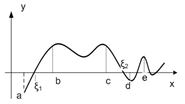
Действительно, если условия теоремы выполнены, как это имеет место на отрезке [a;b] (рис. 6.2.2-3), то есть f(a)∙f(b)<0 и f'(x)>0 для xÎ [a;b], то график функции пересекает ось 0Х только один раз и, следовательно, на отрезке [a;b] имеется один корень 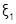уравнения f(x) = 0. Аналогично можно доказать единственность корня 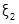на отрезке [c;d], 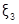на[d;e]и т.д

Рис. 6.2.2-3

Таким образом, для отделения корней нелинейного уравнения необходимо найти отрезки, в пределах которых функция монотонна и изменяет свой знак. Принимая во внимание, что непрерывная функция монотонна в интервалах между критическими точками, при аналитическом отделении корней уравнения можно рекомендовать следующий порядок действий:

1) установить область определения функции;

2) определить критические точки функции, решив уравнение f¢(x)=0;

3) составить таблицу знаков функции f(x) в критических точках и на границах области определения;

4) определить интервалы, на концах которых функция принимает разные знаки.

Пример 6.2.2-3. Отделить корни уравнения x - ln(x+2) = 0.

Область допустимых значений функции f(x) = x - ln(x+2) лежит в интервале (-2; ∞), найденных из условия x+2>0. Приравняв производную f¢(x)=1-1/(x+2) к нулю, найдем критическую точку х_k= -1. Эти данные сведены в табл. 6.2.2-1 и табл. 6.2.2-2 знаков функции f(x).

Таблица 6.2.2-1 Таблица 6.2.2-.2

x	x→-2	-1	x→∞		x	-1.9	-1.1	-0.9	2.0
Sign(f(x))	+	-	+		Sign(f(x))	+	-	-	+

Уравнение x - ln(x+2) = 0 имеет два корня 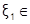(-2;-1]и 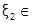[-1; ∞). Проверка знака функции внутри каждого из полученных полуинтервалов (табл.6.2.2) позволяет отделить корни уравнения на достаточно узких отрезках 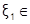[-1.9;-1.1]и 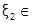[-0.9;2.0].

Дата добавления: 2014-12-27