Метод итерации

Метод итераций предполагает замену уравнения f(x)=0 равносильным уравнением x=j(x). Если корень уравнения отделен на отрезке [a;b], то исходя из начального приближения x₀Î[a;b ], можно получить последовательность приближений к корню

x₁ = j(x₀), x₂ = j(x₁), …, , ( 6.2.3-3 )

где функция j(x) называется итерирующей функцией.

Условие сходимости метода простой итерации определяется следующей теоремой.

Пусть корень х* уравнения x=j(x) отделен на отрезке [a;b] и построена последовательность приближений по правилу x_n=j(x_n-1). Тогда, если все члены последовательности x_n=j(x_n-1) Î [a;b] и существует такое q (0<q<1), что для всех х Î [a; b] выполняется |j’(x)| = q<1, то эта последовательность является сходящейся и пределом последовательности является значение корня x*, т.е. процесс итерации сходится к корню уравнения независимо от начального приближения.

Таким образом, если выполняется условие сходимости метода итераций, то последовательность x₀, x₁, x₂, …, x_n,…, полученная с помощью формулы x_n+1 = j(x_n ), сходится к точному значению корня :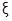

если

Условие j(x)Î[a;b] при xÎ[a;b] означает, что все приближения x₁, x₂, …, x_n,…, полученные по итерационной формуле, должны принадлежать отрезку [a;b], на котором отделен корень.

Для оценки погрешности метода итерации справедливо условие

(6.2.3-4)

За число q можно принимать наибольшее значение |j'(x)|, а процесс итераций следует продолжать до тех пор, пока не выполнится неравенство

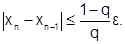(6.2.3-5)

На практике часто используется упрощенная формула оценки погрешности. Например, если 0<q£½ то |x_n-1 - x_n| £ .

Геометрическая иллюстрация метода итераций. Построим на плоскости X0Y графики функций y=x и y=j(x ). Корень уравнения х=j(x) является абсциссой точки пересечения графиков функции y = j(x ) и прямой y=x. Возьмем некоторое начальное приближение x₀ Î [a;b]. На кривой y = j(x) ему соответствует точка А₀ = j(x₀). Чтобы найти очередное приближение, проведем через точку А₀ прямую горизонтальную линию до пересечения с прямой y = x (точкаВ₁) и опустим перпендикуляр до пересечения с кривой (точкаА₁), то есть х₁=j(x₀). Продолжив построение аналогичным образом, имеем ломаную линию А₀, В₁, А₁, В₂, А₂…, для которой общие абсциссы точек представляют собой последовательное приближение х₁, х₂, …, х_n («лестницу») к корню х*. Из рис. 6.2.3-3а видно, что процесс сходится к корню уравнения.

Рассмотрим теперь другой вид кривой y = j(x) (рис. 6.2.6b). В данном случае ломаная линия А₀, В₁, А₁, В₂, А₂…имеет вид “спирали”, и в этом случае наблюдается сходимость.

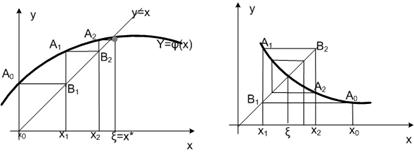
a) b)

Рис. 6.2.3-3

Нетрудно видеть, что в первом случае для производной выполняется условие 0< j’(x)< 1, а во втором случае производная j’(x)<0иj’(x)>-1. Таким образом, очевидно, что если |j’(x)|<1, то процесс итераций сходится к корню.

Теперь рассмотрим случаи, когда |j’(x) |> 1. На рис. 6.2.3-4а показан случай, когда j’(x)>1, а на рис. 6.2.3-4b – когда j’(x) < -1. В обоих случаях процесс итерации расходится, то есть, полученное на очередной итерации значение х все дальше удаляется от истинного значения корня.

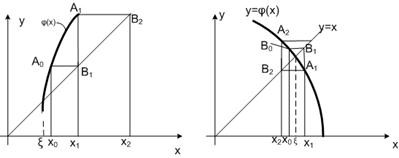
a) b)

Рис. 6.2.3-4

Способы улучшения сходимости процесса итераций. Рассмотрим два варианта представления функции j(x) при переходе от уравнения f(x)кx=j(x).

1. Пусть функция j(x) дифференцируема и монотонна в окрестностях корня и существует числоk £ |j‘(x)|, где k ³ 1 (т.е. процесс расходится). Заменим уравнение х=j(x) эквивалентным ему уравнением х=Y(х ), где Y(х) = 1/j(x) (перейдем к обратной функции). Тогда

а значит q=1/k < 1 и процесс будет сходиться.

2. Представим функцию j(x) как j(x) = х - lf(x), где l - коэффициент, не равный

нулю. Для того чтобы процесс сходился, необходимо, чтобы
0<|j¢(x)| = |1 - lf¢(x)| < 1. Возьмем l= 2/(m₁+M₁ ), где m₁ и M₁ – минимальное и максимальное значения f’(x) (m₁=min|f’(x)|, M₁=max|f’(x)|) для хÎ[a;b], т.е. 0£ m₁ £ f¢(x) £ M₁£1. Тогда

и процесс будет сходящимся, рекуррентная формула имеет вид

Если f¢(x) < 0, то в рекуррентной формуле f(x) следует умножить на - 1.

Параметр λ может быть также определен по правилу:

Если , то , а если , то , где .

Пример 6.2.3-2. Уточнить корень уравнения 5x – 8∙ln(x) – 8 =0 с точностью 0.1, который локализован на отрезке [3;4].

Приведем уравнение к виду, удобному для итераций:

Следовательно, за приближенное значение корня уравнения принимаем значение x₃=3.6892, обеспечивающее требуемую точность вычислений. В этой точке f(x₃)=0.0027.

Дата добавления: 2014-12-27