Метод Ньютона (метод касательных)

Пусть корень уравнения f(x)=0 отделен на отрезке [a;b], причем первая и вторая производные f’(x) и f''(x) непрерывны и знакопостоянны при хÎ [a;b ].

Пусть на некотором шаге уточнения корня получено (выбрано) очередное приближение к корню х_n. Тогда предположим, что следующее приближение, полученное с помощью поправки h_n, приводит к точному значению корня

x = х_n + h_n. (6.2.3-6)

Считая h_n малой величиной, представим f(х_n+ h_n) в виде ряда Тейлора, ограничиваясь линейными слагаемыми

f(х_n + h_n)» f(х_n) + h_nf’(х_n). (6.2.3-7)

Учитывая, что f(x) = f(х_n + h_n) = 0, получим f(х_n) + h_nf ’(х_n)» 0.

Отсюда h_n» - f(х_n)/ f’(х_n). Подставим значение h_n в (6.2.3-6) и вместо точного значения корня x получим очередное приближение

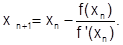(6.2.3-8)

Формула (6.2.3-8) позволяет получить последовательность приближений х₁,х₂, х₃…, которая при определенных условиях сходится к точному значению корня x, то есть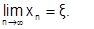

Геометрическая интерпретация метода Ньютона состоит в следующем
(рис.6.2.3-6). Примем за начальное приближение x₀ правый конец отрезка b и в соответствующей точке В₀ на графике функции y = f(x) построим касательную. Точка пересечения касательной с осью абсцисс принимается за новое более точное приближение х₁. Многократное повторение этой процедуры позволяет получить последовательность приближений х₀, х₁, х_{2 ,. . .,} которая стремится к точному значению корня x.

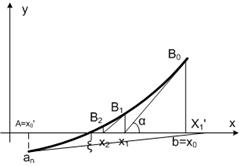
Рис. 6.2.3-6

Расчетная формула метода Ньютона (6.2.3-8) может быть получена из геометрического построения. Так в прямоугольном треугольнике х₀В₀х₁катет
х₀х₁ = х₀В₀/tga. Учитывая, что точка В₀находится на графике функции f(x), а гипотенуза образована касательной к графику f(x) в точке В₀, получим

(6.2.3-9)

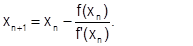(6.2.3-10)

Эта формула совпадает с (6.2.3-8) для n-го приближения.

Из рис.6.2.3-6 видно, что выбор в качестве начального приближения точки а может привести к тому, что следующее приближение х₁окажется вне отрезка [a;b], на котором отделен корень x. В этом случае сходимость процесса не гарантирована. В общем случае выбор начального приближения производится в соответствии со следующим правилом: за начальное приближение следует принять такую точку х₀Î[a;b], в которой f(х₀)×f’’(х₀)>0, то есть знаки функции и ее второй производной совпадают.

Условия сходимости метода Ньютона сформулированы в следующей теореме.

Если корень уравнения отделен на отрезке [a;b], причем f’(х₀)и f’’(х) отличны от нуля и сохраняют свои знаки при хÎ[a;b ], то, если выбрать в качестве начального приближения такую точку х₀Î[a;b], что f(х₀).f¢¢(х₀)>0, то корень уравнения f(x)=0 может быть вычислен с любой степенью точности.

Оценка погрешности метода Ньютона определяется следующим выражением:

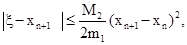(6.2.3-11)

где 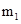- наименьшее значение 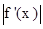при 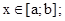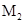- наибольшее значение 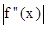при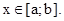

Процесс вычислений прекращается, если 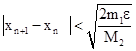, где 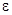-- заданная точность.

Кроме того, условием достижения заданной точности при уточнении корня методом Ньютона могут служить следующие выражения:

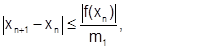
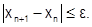(6.2.3-12)

Пример 6.2.3-3. Уточнить методом Ньютона корни уравнения x-ln(x+2) = 0 при условии, что корни этого уравнения отделены на отрезках x₁Î[-1.9;-1.1] и x₂Î [-0.9;2].

Первая производная f’(x) = 1 – 1/(x+2) сохраняет свой знак на каждом из отрезков:

f’(x)<0 при хÎ [-1.9; -1.1],

f’(x)>0 при хÎ [-0.9; 2].

Вторая производная f'(x) = 1/(x+2)² > 0 при любых х.

Таким образом, условия сходимости выполняются. Поскольку f''(x)>0 на всей области допустимых значений, то для уточнения корня за начальное приближение x₁ выберем х₀= -1,9 (так как f(-1,9)×f”(-1.9)>0). Получим последовательность приближений:

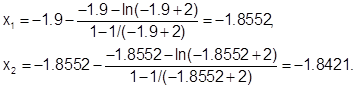
Продолжая вычисления, получим следующую последовательность первых четырех приближений: -1.9; –1.8552, -1.8421; -1.8414. Значение функции f(x) в точке x = -1.8414 равно f(-1.8414) = -0.00003.

Для уточнения корня x₂Î[-0.9;2] выберем в качестве начального приближения х₀ = 2 (f(2)×f”(2)>0). Исходя из х₀ = 2, получим последовательность приближений: 2.0; 1.1817; 1.1462; 1.1461. Значение f(x) в точке x = 1.1461 равно f(1.1461) = -0.00006.

Метод Ньютона обладает высокой скоростью сходимости, однако на каждом шаге он требует вычисления не только значения функции, но и ее производной.

Дата добавления: 2014-12-27