Уравнение прямой для этого случая имеет вид

Метод хорд

Геометрическая интерпретация метода хорд состоит в следующем
(рис.6.2.3-8).

Проведем отрезок прямой через точки A и B. Очередное приближение x₁ является абсциссой точки пересечения хорды с осью 0х. Построим уравнение отрезка прямой АВ:

Рис.6.2.3-8

Положим y = 0 и найдем значение х = х₁ (очередное приближение):

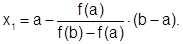
Повторим процесс вычислений для получения очередного приближения - х₂:

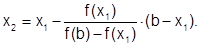
В нашем случае (рис.6.2.3-8) и расчетная формула метода хорд имеет вид

(6.2.3-13)

Эта формула справедлива, когда за неподвижную точку принимается точка b, а в качестве начального приближения выступает точка a.

Рассмотрим другой случай (рис. 6.2.3-9), когда .

Рис.6.2.3-9

Очередное приближение х₁ при y = 0

Тогда рекуррентная формула метода хорд для этого случая имеет вид

(6.2.3-14)

Следует отметить, что за неподвижную точку в методе хорд выбирают тот конец отрезка [a;b], для которого выполняется условие f (x)∙ f¢¢ (x)>0.

Таким образом, если за неподвижную точку приняли точку а, то в качестве начального приближения выступает х₀ = b, и наоборот.

Достаточные условия, которые обеспечивают вычисление корня уравнения f(x)=0 по формуле хорд, будут теми же, что и для метода касательных (метод Ньютона), только вместо начального приближения выбирается неподвижная точка. Метод хорд является модификацией метода Ньютона. Разница состоит в том, что в качестве очередного приближения в методе Ньютона выступает точка пересечения касательной с осью 0Х, а в методе хорд – точка пересечения хорды с осью 0Х – приближения сходятся к корню с разных сторон.

Оценка погрешности метода хорд определяется выражением

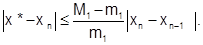(6.2.3-15)

Условие окончания процесса итераций по методу хорд

(6.2.3-16)

В случае, если M₁<2m₁, то для оценки погрешности метода может быть использована формула | x_n - x_n-1| £ e.

Пример 6.2.3-4. Уточнить корень уравнения e^x – 3x = 0, отделенный на отрезке [0;1] с точностью 10^-4.

Проверим условие сходимости:

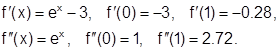
Следовательно, за неподвижную точку следует выбрать а=0, а в качестве начального приближения принять х₀=1, поскольку f(0)=1>0 и f(0)*f"(0)>0.

Результаты расчета, полученные с использованием формулы
6.2.3-14, представлены в таблице 6.2.3-4.

Таблица 6.2.3-4

i	x	f(x)
	0.7812	-0.1569
	0.6733	-0.0591
	0.6356	-0.0182
…	………..	………..
	0.6191	-4.147∙10^-5

Требуемая точность достигается на 8-й итерации. Следовательно, за приближенное значение корня можно принять х = 0.6191.

Дата добавления: 2014-12-27