Метод наименьших квадратов. Одним из способов определения параметров эмпирической формулы является метод наименьших квадратов

Одним из способов определения параметров эмпирической формулы является метод наименьших квадратов. В этом методе параметры a₀, a₁,..., a_nопределяются из условия минимума суммы квадратов отклонений аппроксимирующей функции от табличных данных.

Вектор коэффициентов a^T определяют из условия минимизации

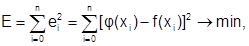
где (n+1) – количество узловых точек.

Условие минимума функции Е приводит к системе линейных уравнений относительно параметров a₀, a₁,..., a_m. Эта система называется системой нормальных уравнений, её матрица – матрица Грама. Элементами матрицы Грама являются суммы скалярных произведений базисных функций

Для получения искомых значений параметров следует составить и решить систему (m+1) уравнения

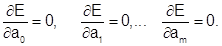
Пусть в качестве аппроксимирующей функции выбрана линейная зависимость y= a₀+a₁x. Тогда

.

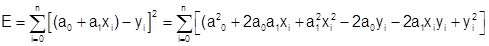Условия минимума:

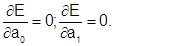
Тогда первое уравнение имеет вид

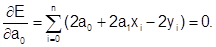
Раскрывая скобки и разделив на постоянный коэффициент, получим

.

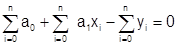Первое уравнение принимает следующий окончательный вид:

.

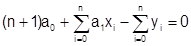Для получения второго уравнения, приравняем нулю частную производную по а1:

. .

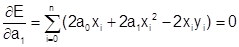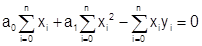Система линейных уравнений для нахождения коэффициентов многочлена 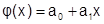(линейная аппроксимация):

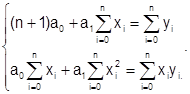
Введем следующие обозначения 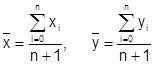- средние значения исходных данных. Во введенных обозначениях решениями системы являются

.

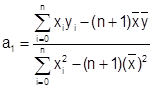В случае применения метода наименьших квадратов для определения коэффициентов аппроксимирующего многочлена второй степени y=a₀+a₁x+а₂х² критерий минимизации имеет вид .

Из условия 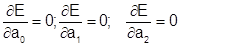получим следующую систему уравнений:

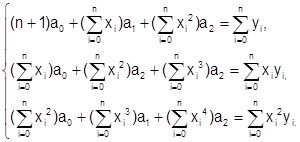
Решение этой системы уравнений относительно а₀, а₁, а₂ позволяет найти коэффициенты эмпирической формулы 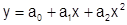- аппроксимирующего многочлена 2-го порядка. При решении системы уравнений могут быть применены численные методы.

В случае степенного базиса (степень аппроксимирующего полинома равна m) матрица Грама системы нормальных уравнений G и столбец правых частей системы нормальных уравнений имеют вид

G =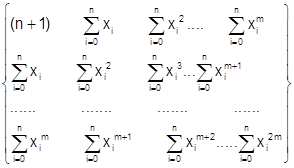

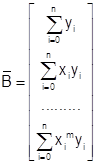
В матричной форме система нормальных уравнений примет вид:

.

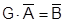Решение системы нормальных уравнений

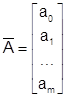найдется из выражения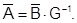

В качестве меры уклонения заданных значений функции y₀, y₁,..., y_n от многочлена степени m - φ(x)=a₀ φ₀(x)+a₁ φ₁(x)+...+a_m φ_m(x), принимается величина

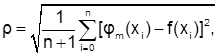
(n+1) – количество узлов, m – степень аппроксимирующего многочлена, n+1>=m.

Дата добавления: 2014-12-27