Метод дихотомии

Пусть дана функция f(x), унимодальная на отрезке [a;b]. Обозначим a₀ = a и
b₀ = b. Поиск минимума начинают с выбора на отрезке неопределенности [a₀;b₀ ] двух симметричных относительно середины точек:

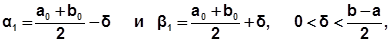где d - параметр метода.

Сравнивая вычисленные в точках a₁ и b₁ значения функций f(a₁) и f(b₁), в силу унимодальности функции можно провести сокращение отрезка неопределенности следующим образом:

1) если f(a₁) £ f(b₁), то x*Î[a₀;b₁] (Рис. 6.6.1-3.а);

2) если f(a₁) > f(b₁), то x*Î[a₁;b₀] (Рис. 6.6.1-3.b).

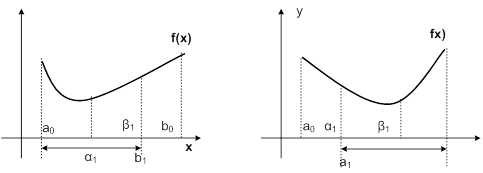
а) b)

Рис. 6.6.1-3

Если описанную процедуру принять за одну итерацию, то алгоритм поиска минимума можно описать следующим образом. Опишем k+1 итерацию, исходя из того, что k -й отрезок неопределенности найден [a_k;b_k]:

1. Вычисляются

2. Находят значения f(a_k+1) и f(b_k+1).

3. Находят k+1 -й отрезок неопределенности по правилу:

если f(a_k+1) > f(b_k+1), то x* Î[a_k+1;b_k],

если f(a_k+1) £ f(b_k+1), то x*Î[a_k;b_k+1]).

Вычисления проводятся до тех пор, пока не выполнится неравенство

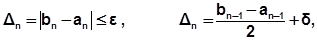
где D_n – длина n -го отрезка неопределенности.

Заметим, что от итерации к итерации D_n убывает и при n®¥ стремится к величине 2d, оставаясь больше этой величины. Поэтому добиться при некотором значении n длины отрезка неопределенности меньше 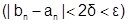заданной точности можно лишь выбирая 0<d<e/2.

Длину конечного интервала неопределенности, обеспечивающего заданную величину e, можно вычислить по формуле

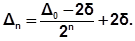
Положив D_n = e, можно определить соответствующее количество итераций:

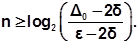
Пример 6.6.2-1. Найти минимум функции f(x)=x³-x+e^-х на отрезке [0;1] c точностью e и вычислить количество итераций, требуемое для обеспечения точности.

Выберем d =0.001 и положим a = 0; b = 1;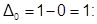

n	a	b	a1	b1	f(a1)	f(b1)	Dn
			0.499	0.501	0.23239	0.23067	0.501
	0.499		0.7485	0.7505	0.14392	0.14435	0.2515
	0.499	0.7505	0.62375	0.6257	0.15486	0.15413	0.12675
	0.62375	0.7505	0.68613	0.6881	0.14040	0.14023	0.06437
…	…..	…..	…..	….	…..	…..	….
	0.701719	0.71931	0.70951	0.7115	0.13954	0.13959	0.00979

При e = 0.1 x*=0.7183 f(x*)=0.1399, а при e = 0.01 x*=0.7066 f(x*)=0.13951.

Дата добавления: 2014-12-27