Технология решения обыкновенных дифференциальных уравнений средствами математических пакетов

Сравнение методов решения ОДУ

Метод Эйлера является простейшим одношаговым методом. Однако его низкая точность (погрешность убывает пропорционально величине шага) служит серьезным препятствием для его использования на практике. Увеличение точности за счет уменьшения шага, к сожалению, приводит к росту количества итераций и соответственно увеличению ее составляющей погрешности – погрешности вычисления. Метод имеет первый порядок точности, соответствующий используемому в нем методу левых прямоугольников.

Метод «прогноза и коррекции» позволяет уточнить расчетную формулу за счет «прогноза» значения в следующей точке, полученного на первом этапе по формуле Эйлера, и «коррекции» - усреднения углового коэффициента – на втором этапе. Этот метод имеет второй порядок точности, поскольку для вычисления интеграла при вычислении приращения использована формула трапеций. По сравнению с методом Эйлера, метод «прогноза и коррекции» требует меньшее количество итераций для обеспечения заданной точности

Наиболее популярными среди классических одношаговых методов решения ОДУ являются методы Рунге-Кутты четвертого порядка. При этом метод Эйлера и метод «прогноза и коррекции» можно рассматривать как простейших представителей методов Рунге-Кутты. Методы Рунге-Кутты четвертого порядка эффективны и, если отрезок интегрирования не очень велик, обеспечивают сравнительно высокую точность.

Обеспечение требуемой точности решения ОДУ достигается применением в расчетах метода автоматического выбора шага, в котором для оценки локальной погрешности (погрешности на каждом шаге решения) используется правило Рунге.

При решении ОДУ его следует привести к нормальной форме (к виду разрешенному относительно производной исходного ОДУ)

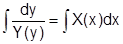Для ОДУ с разделяющимися переменными исходное уравнение можно привести к виду , тогда выражение задает решение задачи Коши с начальными условиями 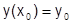как функцию y от переменной х.

Пример 6.5.6-1. Решить ОДУ вида .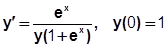

Найдем частное решение данного ОДУ с использованием средств Mathcad, сначала методом разделения переменных, а затем с использованием функции odesolve(x, xk, n), где х – имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования, n – количество шагов, на которых вычисляется решение ОДУ. Результаты подтверждают правильность преобразований.

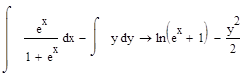
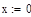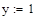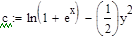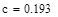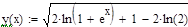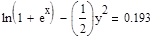
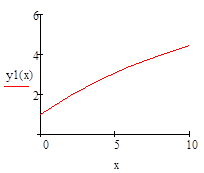
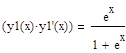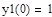произвольная постоянная   Аналитическое решение ОДУ 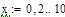Численное решение ОДУ

Аналитическое выражение для решений ОДУ удается получить достаточно редко, поэтому широкое распространение при решении ОДУ получили численные методы.

Пример 6.5.6-2. Решить ОДУ 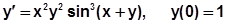на отрезке [0;3] методами Рунге-Кутты с постоянным шагом h=0,6.

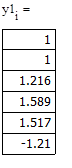
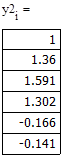
В приведенном ниже документе решение, полученное методом Эйлера, обозначено как y1, методом Рунге-Кутты 2-го порядка – y2, а 4-го порядка – y4.

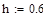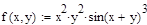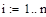
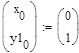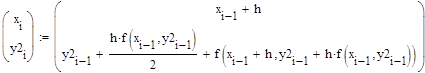Метод Эйлера Метод Рунге-Кутты 2-го порядка 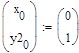Метод Рунге-Кутты 4-го порядка

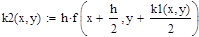
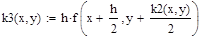
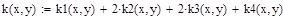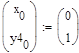
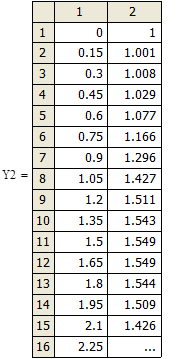
В Mathcad нет средств символьного решения ОДУ, но достаточно широко представлены методы численного решения задачи Коши. Для этого предназначена, например, функция rkfixed(y, x₀, x_end, N, D), где y – первоначально равно y₀, x₀ и x_end – начальное и конечное значения аргумента, N – количество проводимых вычислений решения, а переменной D(x,y) должно быть присвоено выражение для вычисления правой части уравнения. Результатом вычислений функции rkfixed() служит матрица, в первом столбце которой содержатся координаты узлов x₀ … x_end, а во втором – значения приближенного решения в соответствующих узлах. В функции rkfixed() вместо метода Рунге-Кутты используется метод Булирша-Штера. Ниже приведены решения и их графическая иллюстрация, полученные с шагом 0.6 и 0.15.

Пример 6.5.6-3. Решить ОДУ у’= 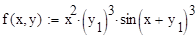на отрезке [0;3] методами Рунге-Кутты с постоянным шагом h=0.6 и h=0.15.

 

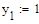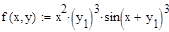
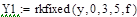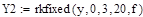
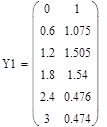
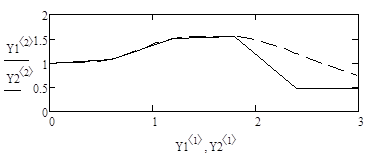
Решение ОДУ 2-го порядка вида у”=F(x, y, z), где z=y’ также может быть получено методом Рунге-Кутты 4-го порядка. Ниже приведены формулы для решения ОДУ:

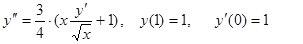
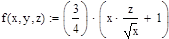
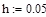
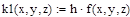
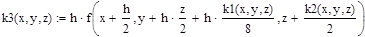
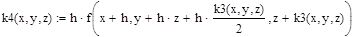
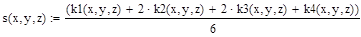
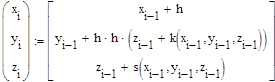
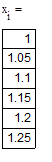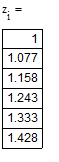
Система Mathcad имеет специальную встроенную функцию для решения дифференциальных уравнений. Она имеет вид: Odesolve (x, b [, steps ]).

Для решения задачи Коши необходимы так называемые начальные условия и указание конца интервала. Эти данные вместе с самим уравнением записываются в блок функции Given, и лишь затем применяется сама функция odesolve(). Функция имеет ряд особенностей. Если указано число шагов step, то решение выполняется с фиксированным шагом, иначе - адаптивным методом.

Дата добавления: 2014-12-27