Исследование структуры данных

Факторный анализ

Собирая данные, исследователь руководствуется определенными гипотезами. Полученная в ходе исследования информация относится к избранным предмету и теме исследования, но нередко она представляет собой сырой материал, в котором можно изучить структуру показателей, характеризующих объекты, а также выявить однородные группы объектов. Информацию лучше представить в геометрическом пространстве, лаконично отразить ее особенности в классификации объектов и переменных. Такая работа создает предпосылки к выявлению типологий объектов и формулированию «социального пространства», в котором обозначены расстояния между объектами наблюдения, позволяет наглядно представить свойства объектов.

Факторный анализ является одним из наиболее мощных статистических средств анализа данных. В его основе лежит процедура объединения групп коррелирующих друг с другом переменных («корреляционных узлов») в несколько факторов.

Цель факторного анализа – сконцентрировать исходную информацию, выражая большое число рассматриваемых признаков через меньшее число более емких внутренних характеристики, которые, однако, не поддаются непосредственному измерению (являются латентными).

Факторный метод будет изложен на примере опроса, проведенного с целью выяснения политических ориентаций жителей города. В ходе опроса респондентам предложили выбрать высказывания, соответствующие их мнению, и отдать свой голос в поддержку тех, кто:

1. согласен с нынешним политическим курсом (var 21.1)

2. выступает с критикой нынешнего политического курса (var 21.2)

3. выступает за вхождение России в западную цивилизацию (var 22.1)

4. против сближения России с Западом (var 22.2)

5. выступает за неведение жесткого порядка (var 23.1)

6. считает главным демократию, политические и личные свободы граждан (var 23.2)

7. выступает за усиление влияния Церкви на государство (var 24.1)

8. считает, что государство и Церковь не должны вмешиваться в жизнь граждан (var 24.2)

9. считает, что государство не должно вмешиваться в свободную рыночную экономику (var 25.1)

10. выступает за государственный контроль бизнеса (var 25.2)

11. выступает за объединение граждан в интересах государства (var 26.1)

12. считает, что граждане должны добиваться успеха сами (var 26.2)

Оценки ставились по двухбалльной шкале: 1) поддерживаю, 2) не поддерживаю.

Для факторного анализа:

· Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)

Откроется диалоговое окно Factor Analysis (Факторный анализ)

Переменные var21-….var26 поместите в поле тестируемых переменных и ознакомьтесь с возможностями, предлагаемыми различными кнопками этого диалогового меню.

После щелчка по кнопке Descriptive Statistics (Дескриптивные статистики) оставьте вывод первичных результатов, которые включают в себя первичные относительные дисперсии простых факторов, собственные значения и процентные доли объяснённой дисперсии. Довольно часто бывает необходим также вывод одномерных статистик и корреляционных коэффициентов. В группе Correlation Matrix (Корреляционная матрица) целесообразно отметить флажком KMO and Barltett test of sphericity (Критерии КМО и сферичности Бартлетта), вычисляется два критерия – на многомерную нормальность (Бартлетта) и адекватность выборки (КМО определяет применимость факторного анализа к выбранным переменным).

С помощью кнопки Extraction... (Отбор) можно выбрать метод отбора. Если оставить здесь анализ главных компонентов, установленный по умолчанию, то количество отобранных в этом случае факторов приравнивается к числу собственных значений, превосходящих единицу. Также есть возможность собственноручно указать это количество.

Щёлкните на выключателе Extraction... (Извлечение), оставьте установку Principal components (Анализ главных компонентов). В нашем примере количество факторов сознательно ограничим тремя. Если бы мы не сделали такого ограничения, то в соответствии с начальными установками было бы создано двенадцать факторов, количество, которое очень тяжело поддаётся обзору.

Можно построить график собственных значений или диаграмму каменистой осыпи, установив флажок на Scree plot. Точками показаны соответствующие собственные значения, в пространстве двух координат. Этот тип диаграммы обычно используется при определении достаточного числа факторов перед вращением. При этом руководствуются следующим правилом: оставлять нужно лишь те факторы, которым соответствуют первые точки на графике до того, как кривая станет более пологой.

Выключатель Rotation... (Вращение) позволяет выбрать метод вращения. Вращение требуется потому, что изначально структура факторов, будучи математически корректной, как правило, трудна для интерпретации. Целью враще ния является получение простой структуры, которой соответствует большое значение нагрузки каждой переменной только по одному фактору и малое по всем остальным факторам.

Факторные нагрузки можно представить как коэффициенты корреляции каждой переменной с каждым из выявленных факторов. Чем теснее связь переменной с рассматриваемым фактором, тем выше значение факторной нагрузки. Положительный знак факторной нагрузки указывает на прямую, а отрицательный знак – на обратную связь переменной с фактором.

Активируйте метод варимакса (Varimax) и оставьте активированным вывод повёрнутой матрицы факторов. Далее вы можете организовать вывод факторных нагрузок в графическом виде, в котором первые три фактора будут представлены в трёхмерном пространстве; в случае наличия только двух факторов в слое приводится только одно изображение. При этом установите флажок на Loading plot(s).

Если Вы хотите найти значения факторов и сохранить их в виде дополнительных переменных задействуйте выключатель Scores... (Значения) и отметьте Save as variables (Сохранить как переменные). По умолчанию установлен регрессионный метод.

Выключатель Options... (Опции) предназначен для обработки пропущенных значений. Здесь обеспечивается возможность заменить пропущенные значения средними значениями соответствующих переменных.

При факторном анализе постоянно появляются сообщения об ошибках, например 2,56Е-02 и т.п. Действительно такой формат вывода в глазах непосвященного пользователя очень портит картину всей таблицы. Это, так называемый, Е-формат, знакомый всем программистам по языку Фортран (Fortran), где буква Е соответствует 10 в некоторой степени; для числа 2,5Е-02 можно было бы записать и 0,0256.

Можно запретить вывод малых факторных нагрузок и для этого установим граничное значение выводимых нагрузок равным 0,4. Достоинство этого шага состоит в том, что устраняется непривлекательное отображение малых значений в Е-формате. Для этого активируйте опцию Suppress absolute values less then: (He выводить абсолютные значения меньшие, чем:) и введите предельное значение 0,4.

· Для проведения расчётов щёлкните на ОК.

·

В окне обзора появятся результаты. Сначала приводятся первичные статистики: Критерий сферичности Бартлетта показывает статистически достоверный результат (p < 0,05), данные вполне приемлемы для факторного анализа.

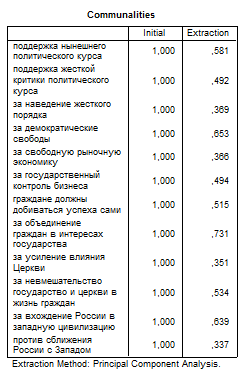
В таблице Communalities перечислены переменные и общности. Столбцы второй таблицы Total Variance Explained содержат характеристики выделенных факторов: их порядковые номера, суммы квадратов нагрузок, процент общей дисперсии, обусловленной фактором, и соответствующий кумулятивный (накопленный) процент (до и после вращения). Чем больше процент дисперсии, обусловленный фактором, тем больший вес имеет данный фактор. А чем больше кумулятивный процент, накопленный к последнему фактору, тем более состоятельным является факторное решение. Если он составляет менее 50%, следует либо сократить количество переменных, либо увеличить количество факторов.

В данном примере насчитывается шесть собственных значений, превосходящих единицу, что означало бы отбор шести факторов, если бы мы не изменили установку по умолчанию Eigenvalues over: 1 (Собственные значения, превосходящие единицу) и не ограничили бы количество рассматриваемых факторов тремя.

В качестве вспомогательного средства для определения задаваемого числа факторов может послужить специальная точечная диаграмма. Слово Screeplot, употребляемое для обозначения этой диаграммы состоит из двух частей: английского слова scree, что означает щебень и слова plot, что в английском соответствует графическому представлению. Такая диаграмма служит для того, чтобы маловажные факторы — щебень — можно было отделить от самых значимых факторов. Эти значимые факторы на графике образовывают своего рода склон, то есть ту часть линии, которая характеризуется крутым подъёмом. В приведенной диаграмме такой крутой подъём наблюдается в области первых восьми факторов.

Если посмотреть на график, то можно заметить что склон, то есть область значимых факторов, наблюдается выше восьмого фактора (восьмой, седьмой, шестой, пятый...), а ниже восьмого фактора (девятый, десятый, одиннадцатый, двенадцатый...) расположился щебень, область незначимых факторов. Можно самостоятельно провести расчет с использованием модели, включающей различное число факторов; в рассмотренном примере было бы уместным произвести сравнение моделей с учётом восьми, семи и шести факторов.

Программа SPSS включает в вывод исходную структуру факторных нагрузок (до вращения). Эти данные в большинстве случаев не представляют интереса, для нас более важна таблица Rotated Component Matrix (Матрица перевернутых компонент).

Здесь начинается самая интересная часть факторного анализа: мы должны попытаться объяснить отобранные факторы. Для этого в каждой строке повёрнутой факторной матрицы нужно отметить ту факторную нагрузку, которая имеет наибольшее абсолютное значение.

Эти факторные нагрузки следует понимать как корреляционные коэффициенты между переменными и факторами. Так переменная var21.1 сильнее всего коррелирует с фактором 2, а именно, величина корреляции составляет 0,549, переменная var21.2 сильнее всего коррелирует с фактором 1 (0,589), переменная же var22.1 коррелирует сильнее всего с фактором 1 (0,356) и т.д. В большинстве случаев включение отдельной переменной в один фактор, осуществляемое на основе коэффициентов корреляции, является однозначным. В исключительных случаях, переменная может относиться к двум факторам одновременно. Могут быть также и переменные, которыми нельзя нагрузить ни один из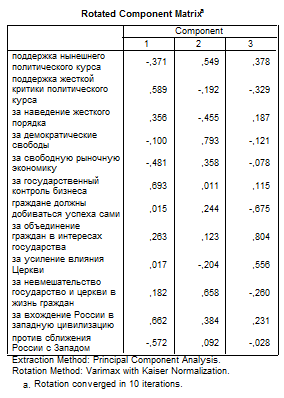
отобранных факторов.

Варианты мнений, указанные вначале рассмотрения примера, можно отнести в следующем порядке к двум факторам:

Фактор 1:

1. поддержка жесткой критики политического курса (var21.2);

2. за наведение жесткого порядка (var 23.1);

3. за государственный контроль бизнеса (var25.2);

4. за вхождение Россию в западную цивилизацию (var 22.2).

Фактор 2:

1. поддержка нынешнего политического курса (var21.1);

2. за демократические свободы (var 23.2);

3. за свободную рыночную экономику (var 25.1);

4. граждане должны добиваться успеха сами (var 26.2);

5. против сближения России с Западом (var21.2);

6. за невмешательство государства и церкви в жизнь граждан (var 24.2);

Фактор 3

1. за объединение граждан в интересах государства(var 26.1);

2. за усиление влияния Церкви (var 24.1).

Ниже расположены диаграммы, где представлены факторные нагрузки трех и двух факторов.

Для интерпретации факторов было бы оптимально, если бы точки лежали ближе к осям и подальше от точки начала отсчёта; тогда каждая переменная имела бы значительную нагрузку для одного фактора и незначительную для другого.

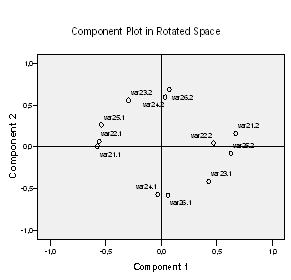
В соответствии с порядком изложения наши три сгруппированных фактора можно кратко охарактеризовать при помощи следующих выражений: «правые государственники», «либералы», «консерваторы». Однако столь явно, как в приведенном примере факторы удаётся объяснить не всегда. Если нет возможности провести вербальное объяснение факторов, то факторный анализ можно считать неудавшимся.

Дата добавления: 2014-12-27