Аппроксимация функций методом наименьших квадратов

В прикладных задачах бывает необходимо аппроксимировать функцию единым аналитическим выражением на большом интервале изменения независимой переменной, что невозможно методами интерполяции. К тому же, если функция определена со значительной случайной погрешностью, то интерполировать ее вообще не имеет смысла. Такая ситуация возникает, например, при аппроксимации результатов экспериментальных исследований механических свойств материалов.

Пусть функция y(x) задана таблично:

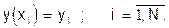(32)

Условие аппроксимации j(x)» y(x) будем понимать как условие минимальности нормы.

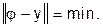(33)

В гильбертовом пространстве L₂(r) функций, интегрируемых с квадратом с весом r(x)>0 на [a, b] норму вводим следующим образом:

(34)

где скалярное произведение определено так:

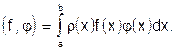(35)

Для таблично заданной функции скалярное произведение имеет вид

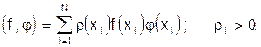(36)

Тогда условие (33) принимает вид условия наилучшего среднеквадратичного приближения

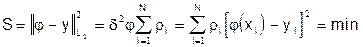(37)

здесь dj — среднеквадратичное уклонение.

Выберем линейную аппроксимацию

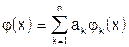(38)

с числом членов n<N. Тогда

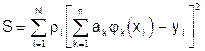(39)

и необходимые условия минимума (37) запишутся в виде системы линейных уравнений относительно искомых констант аппроксимации a_k:

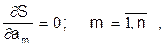(40)

или

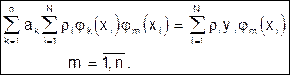(41)

Можно показать, что эти условия минимума являются и достаточными.

Весовая функция r(x_i) должна давать больший вес в тех узлах, в которых нужна большая точность. Обычно 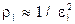где e_i — абсолютная погрешность. Если погрешность по всем узлам одинакова, то r_i=1.

Определенную по всем узлам погрешность интерполяция оценивает по среднеквадратичному уклонению согласно формуле (37):

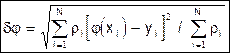(42)

Дата добавления: 2014-12-27