Средняя гармоническая взвешенная

Средняя гармоническая взвешенная

На основе следующих данных рассчитать среднюю заработную плату на одного работника:

Таблица 6.5

Заработная плата, руб. х	Фонд оплаты труда, руб. m = х*f
6 000	30 000
7 000	105 000
8 000	80 000

Для расчета средней заработной платы используется логическая формула

Численность работников неизвестна, но ее можно рассчитать, т. к. известны фонд оплаты труда и заработная плата на одного работника в каждой группе.

где m – готовое произведение вариант на соответствующие им частоты.

Таким образом, средняя гармоническая взвешенная применяется в том случае, когда представлены два ряда данных: варианты и произведения этих вариантов на соответствующие им частоты.

Если возникают затруднения в выборе средних величин, то используют следующие правила:

§ если при умножении вариант на показатели второго ряда данных получается показатель, имеющий экономический смысл, то применяется средняя арифметическая взвешенная;

§ если при делении одного ряда данных на соответствующие им варианты получается показатель, имеющий экономический смысл, то применяется средняя гармоническая взвешенная.

6.6. Структурные средние величины: мода и медиана

Мода (М₀) – это наиболее часто встречающееся значение признака, т. е. значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.

В дискретных вариационных рядах для определения моды не требуется специальных вычислений - значение признака, которому соответствует наибольшая частота, и будет значением моды.

Например, по представленным данным о возрастном составе группы определим моду.

Возраст, лет Численность, человек

х f

19 4

17 13

18 9

21 1

20 3

Здесь наибольшая частота – 13, значит, М_о =17. Таким образом, в группе больше всего студентов, имеющих возраст 17 лет.

Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле.

,

где X_Mo - нижняя граница модального интервала;

d – величина модального интервала;

f_Mo - частота модального интервала;

f_Mo-1 - частота интервала, предшествующего модальному;

f_Mo+1 - частота интервала, следующего за модальным.

Например, имеются данные по группе банков.

Таблица 6.6

Сумма выданных кредитов, млн. руб.	Количество банков
до 40
40-60
60-80
80-100
100-120
120 и выше

Определим модальный размер выданных кредитов:

§ модальным является интервал 60-80, т.к. ему соответствует наибольшая частота (21);

§ нижняя граница модального интервала X_Mo = 60; величина интервала d = 20(80-60);

§ частота модального интервала f_Mo = 21; частота интервала, предшествующего модальному, f_Mo-1 = 15; частота интервала, следующего за модальным = 12.

Подставим в формулу значения

млн. руб.

Медиана – это варианта, находящаяся в середине упорядоченного ряда и делящая его пополам.

Например:

возраст, лет

х

19 - медиана, т.к. это середина упорядоченного ряда.

Если число вариантов четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.

Например, по данным о цене яблок определить медиану:

Таблица 6.7

Номер магазина
Цена яблок, руб. за кг

В середине ранжированного ряда находятся цены двух магазинов.

Медиана определяется как средняя величина из этих значений:

(52+54)/2=53 руб.

Таким образом, в 50% магазинов яблоки продаются по цене не выше

53 руб. за кг, а в других 50% магазинов – по цене не ниже 53 руб.

В дискретных вариационных рядах медиану определяют так:

1) находят ее порядковый номер по формуле

- при четном числе единиц совокупности ;

- при нечетном числе единиц совокупности ;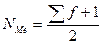

2) строят ряд накопленных частот;

3) находят накопленную частоту, которая равна порядковому номеру медианы или его превышает;

4) варианта, соответствующая данной накопленной частоте, является медианой

Например, на основе данных определим медианный стаж сотрудников страховой компании:

Таблица 6.8

Время работы, лет х	Число сотрудников, чел. f	Накопленная частота S
		5+7=12
		12+4=16
		16+9=25
		25+13=38
		38+10=48
		48+16=64
		64+13=77
Итого		-

Так как число единиц совокупности нечетное (77), то номер медианы определяем по формуле: .

Для того чтобы найти значение варианты, стоящее на 39 месте, рассчитаем накопленные частоты. Искомый 39-й сотрудник входит в шестую группу, т.к. в пятой группе сумма накопленных частот равна 38. Значит, медианный стаж сотрудников равен 6 годам, итак 50% сотрудников имеют стаж работы не более 6 лет, а 50% - 6 лет и более.

Медиана в интервальном вариационном ряду рассчитывается по формуле

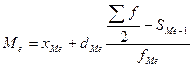
где x_Me - нижняя граница медианного интервала;

d_Me – величина медианного интервала;

S_Me – накопленная частота интервала, предшествующая медианному;

f_Me – частота медианного интервала.

Например, по следующим данным определим медианное значение суммы выданных банками кредитов:

Таблица 6.9

Сумма выданных кредитов, млн. руб.	Количество банков, f	Накопленная частота, S
20-40
40-60
60-80
80-100
100-120
120-140
140-160
Итого		-

- определим порядковый номер медианы

- определим накопленную частоту медианного интервала

_; S_Me =44, т.к. больше 38;

- определим соответствующий ей медианный интервал «60-80»;

- рассчитаем значение медианы по формуле:

,

т.е. у 50% банков сумма выданных кредитов не превышает 74,286 млн. руб.

Дата добавления: 2014-12-23