ВВЕДЕНИЕ 1 страница. весь научный прогресс не что иное, как постепенный отказ от простоты мира

В СОВРЕМЕННОМ ЕСТЕСТВОЗНАНИИ

СТАТИСТИЧЕСКИЙ ПОДХОД В ИСТОРИИ НАУКИ И

Б.В. БУЛЮБАШ

"…весь научный прогресс не что иное, как постепенный отказ от простоты мира..."

Станислав Лем

Изучая значимые для общества проблемы современной науки (генетически модифицированные продукты, глобальное потепление, электросмог…), исследователь сталкивается с большим количеством разнообразной информации. При этом данные, полученные из разных источников и разными методами, нередко противоречат друг другу. В подобных ситуациях неопределенности построить приемлемую модель изучаемого явления крайне сложно (а иногда и невозможно) Анализу таких ситуаций - на примере сюжетов из истории науки и современного естествознания (которое нередко называют естествознанием сложного) – как раз и посвящено данное пособие.

Стремясь выделить нечто общее в разных сюжетах, мы обращаем внимание на то, что исследователи в подобных ситуациях активно используют язык статистического подхода. В этом случае ученый анализирует в первую очередь не столько теории и модели, сколько вероятности, корреляции (статистические зависимости, когда с изменением одного параметра меняется другой), факторы риска, случайные и систематические погрешности. На этом этапе чрезвычайно важной для исследователя становится интуиция…именно интуиция помогает увидеть контуры нового знания в хаосе фактов и чисел.

Структура пособия. Соответственно сказанному во всех пяти главах данного пособия мы обращаем особое внимание на использование естествоиспытателями статистического подхода. При этом в разных сюжетах, разбираемых в данном пособии, уровень использования языка статистики достаточно разный.

В первой главе пособия рассказывается об истории проникновения статистики в гуманитарные и естественные науки. Вторая глава состоит из несколько историко-научных сюжетов (Сноу, Земмельвейс, Пастер), объединенных общей эпохой – 19 веком, а также общей темой – историей создания микробной теории болезней. Глава третья называется "Физика, астрономия и статистика: как случайное отличить от неслучайного?", в ней разобраны истории из научных биографий физиков Джеймса Джоуля, Роберта Милликена и астронома Генриетты Левитт. Четвертая глава "Радон, генетически модифицированные продукты и электросмог: каковы риски?" рассказывает о статистических исследованиях, связанных с возможным влиянием слабых и неионизирующих излучений на организм человека, а также с возможной опасностью использования генетически модифицированных растений. Пятая глава "Климат планеты Земля: задача со многими неизвестными" посвящена дискуссиям вокруг разнообразной статистической информации, связанной с проблемой глобального потепления.

Легко видеть, что с точки зрения содержания разбираемые нами примеры относятся к различным предметным областям. По мнению автора, такая эклектичность неизбежна, поскольку предметом нашего интереса является естествознание – междисциплинарная область знания. Излишне говорить, что разобранные в пособии сюжеты не укладываются в распространенное представление об истории научных открытий как истории рождения идей и последовавших экспериментальных исследований, в которых эти идеи нашли подтверждение.

Насколько соответствуют рассмотренные в пособии примеры тому направлению, в котором развивается наука XXI века? Вот что пишет о современной науке В.В.Свиридов, автор учебника "Концепции современного естествознания" (год издания – 2005, на учебнике - гриф Минобразования РФ):

1. Современное естествознание стало эволюционным, историчным. Уникальность объекта неизбежно требует исторического, эволюционного метода его исследования.

Действительно, только с учетом временных изменений возможен анализ влияния ГМР на человека. Только в контексте эволюции атмосферы Земли за тысячи и сотни тысяч лет возможно обсуждение причин парникового эффекта. Только изучение процессов, происходящих в организме за большие промежутки времени, выявило побочные эффекты борьбы с бактерией хеликобактер. Вне больших временных промежутков невозможно проанализировать проблему влияния радиоактивных излучений на рост раковых клеток.

2. Естествознание все больше интересуется сложными объектами. Естествознание все больше интересуется уникальными объектами, существующими в единственном числе.

В нашем случае такими уникальными (и такими сложными) объектами являются атмосфера и гидросфера Земли (парниковый эффект), а также земная биосфера (генетически модифицированные растения). Несомненно, уникальным объектом является Вселенная (закон Хаббла).

Значительная часть приводимых нами примеров заимствована из британского учебника по естествознанию для "гуманитарного профиля" Science for Public Understanding. Из учебника же заимствована ориентация на такие примеры из истории науки (и из ее настоящего), в которых видна сложность достижения консенсуса внутри научного сообщества. Мы также старались следовать общей стратегии британских коллег, анализирующих в курсе естествознания в первую очередь те научные сюжеты, которые имеют непосредственное отношение к человеку.

Глава 1. Экскурс в историю

"Природа говорит с нами на тысячу голосов и мы лишь недавно начали ее слушать."

Илья Пригожин

Первые примеры использования статистики в естественных науках связаны, что не удивительно, с медициной. Основателем медицинской статистики – а для науки 16 – 17 веков медицина воплощала в себе практически все естественнонаучные дисциплины - считается лондонский торговец Джон Граунт (1620 – 1674). Именно он представил в январе 1662 года президенту Лондонского Королевского общества доклад «Естественные и политические наблюдения…над бюллетенем смертности». Граунт был первым ученым, установившим, что мальчиков рождается больше, чем девочек в отношении 14: 13. Граунт пытался вычислить население Лондона, величина которого была предметом многочисленных слухов (по одному из которых она доходила до 7 миллионов человек). Заслуга Граунта была в том, что он обнаружил, что это число не соответствует числу похорон (менее 17 тысяч в год). Именно в связи с этим Граунт выдвинул гипотезу о том, что численность населения можно вычислять на основе бюллетеней смертности. Для этого надо было знать распределение населения по возрастам и смертность по возрастам. Излишне говорить, что гипотеза Граунта впоследствии подтвердилась.

Именно статистические исследования сделали знаменитым английского священника Томаса Мальтуса (1766 – 1834). Он использовал информацию об изменении численности населения во времени для построения математической модели роста населения. Считая рождаемость (среднее число родившихся в расчете на десять тысяч населения и за единицу времени) и смертность (среднее число умерших в расчете на десять тысяч населения и за единицу времени) постоянными величинами и предполагая, что рождаемость превышает смертность, легко показать, что относительный прирост населения в единицу времени остается величиной постоянной. Чтобы вычислить относительный прирост

некоторой величины за единицу времени, вы должны взять абсолютный прирост этой величины за небольшой промежуток времени, разделить его на значение величины в начале этого промежутка и затем разделить на величину промежутка времени. Математически такой модели соответствует экспоненциальный рост численности населения во времени. Производство же продуктов питания тоже растет во времени (что связано с ростом агротехнической культуры), но, естественно, более медленно, нежели численность населения.

Естественно, в этом пункте и появилось понятие борьбы за существование – иначе говоря, конкуренции людей (и не только людей) за ограниченные ресурсы. Эта идея Мальтуса чрезвычайно сильно повлияла на политическую и экономическую мысль. До него общепринятой была абсолютно противоположная точка зрения точка зрения, согласно которой рост населения - это необходимое условие роста промышленного производства. Таким образом, статистическая информация стала основой математической модели, модель же, в свою очередь, стала основой весьма важных социально-экономических и естественнонаучных выводов. Можно сказать, что модель Мальтуса стала первой удавшейся попыткой математического описания социальных процессов. До Мальтуса математически описать удавалось только движение небесных тел в рамках небесной механики.

Достижения Мальтуса были признаны научным сообществом, в 1805 г. его назначили профессором современной истории и политической экономии во вновь организованном колледже Восточно-Индийской компании в Хайлибери. Фактически Мальтус стал ведущим академическим экономистом Англии. Многие его современники не принимали его точку зрения на судьбы популяций, однако никто не подвергал сомнению его статус выдающегося мыслителя своего времени. С двумя современными (и весьма отличными друг от друга) оценками роли и места Мальтуса с точки зрения современных демографических моделей можно познакомится в статьях известных российских специалистов в области естествознания – доктора физико-математических наук С.П.Капицы[1] и доктора биологических наук, академика РАН Е.Д.Свердлова[2].

По мнению С.П.Капицы, в настоящее время рост населения Земли замедлился и численность населения приближается к некоторому пределу. Е.Д.Свердлов, напротив, считает идеи Мальтуса весьма актуальными в связи с проблемой нехватки ресурсов Земли для обеспечения потребностей всех живущих на ней людей.

Большое впечатление выкладки Мальтуса произвели на Чарльза Дарвина и сама концепция борьбы за существование стала одной из основ теории эволюции. Приведем высказывания Дарвина на этот счет. В октябре 1838, 15 месяцев спустя после того, как я начал мое систематическое исследование, случилось мне прочесть для развлечения Мальтуса о популяциях и, будучи подготовленным к признанию борьбы за существование, которая происходит повсеместно... я моментально понял, что при этом благоприятные варианты будут иметь тенденцию к сохранению, а неблагоприятные - к уничтожению. Результатом будет образование новых видов" ("Автобиография"). "Я увидел при чтении Мальтуса про популяции, что естественный отбор будет неизбежным результатом быстрого роста числа всех живых существ..." ("Изменчивость животных и растений при одомашнивании").

Таким образом, статистическая модель Томаса Мальтуса определила возникновение и развитие одной из самых известных естественнонаучных теорий 19 столетия - теории эволюции Чарльза Дарвина.

Одна из простейших и наиболее распространенных статистических процедур - нахождение среднего значения. Любые измерения, которые выполняет ученый – экспериментатор, предполагают нахождение среднего значения серии измерений. Математическая обработка результатов измерений стала возможной после того появления теории ошибок немецкого математика Карла Фридриха Гаусса (1777 – 1855) В основе теории ошибок (изложенной впервые в 1807 г. в мемуаре Гаусса "Теория движения небесных тел, обращающихся около Солнца по коническим орбитам") лежит нормальный закон распределения вероятностей случайных ошибок (знаменитое распределение Гаусса). Распределение Гаусса показано на рис.1. По оси абсцисс отложено численное значение погрешности X, равное разности между измеряемой величиной и ее средним значением, по оси ординат - так называемая “плотность вероятности”. Смысл плотности вероятности следующий. Вероятность того, что погрешность будет находится в интервале между X1 и X1 + dX. численно равна площади, ограниченной кривой, осью абсцисс и прямыми X = X1 и X = X1 + dX.

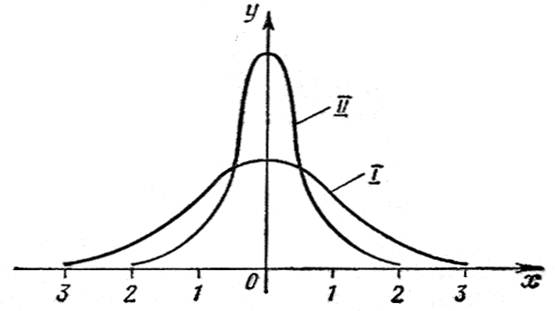
Рис. 1 Распределение Гаусса

Точность измерений может быть разной – серии более точных измерений соответствует "более острое" распределение Гаусса (II), серии менее точных измерений - менее острое(I). На языке теории ошибок это означает, что у распределений будут разные дисперсии. Распределению с отчетливо выраженным максимумом (II) соответствует меньшая дисперсия, распределению с более размытым максимумом (I) – большая дисперсия.

Распределение Гаусса наполняет новым содержанием понятие о среднем значении измеряемой величины. Именно среднему значению измеряемой величины соответствует наибольшая плотность вероятности. Иначе говоря, экспериментов, в которых измеренная величина будет не сильно отличаться от среднего значения (соответственно, погрешность будет мала) будет существенно больше, чем тех, в которых измеряемая величина будет существенно отклоняться от среднего значения

В 19 веке идея усреднения разнообразных причин - не сводящаяся к нахождению среднего значения – постепенно проникала в сознание и естественников и гуманитариев. Так, философ Спенсер в 1860 г. предложил рассматривать мозг как усредняющий интересы жизни – физические, интеллектуальные, моральные, социальные». Точно так же он оценивал и функции парламента "как усредняющего интересы различных классов общества". Похожим был и его взгляд на биологию: "форма каждого вида организмов – результат усредненной игры внешних сил, действовавших в течение его эволюции как вида". Бельгиец Адольф Кетле (1796 – 1874) активно способствовал популяризации идей статистики, и особенно концепции "среднего человека". По его словам, характеристики "среднего человека" остаются неизменными; индивидуальностей же следует рассматривать как отклонения от него. Именно в изучении "среднего человека" Кетле видел главную цель статистики.

Весьма много сил Кетле потратил на попытки применить статистические методы в изучении преступности и здесь у него нашелся последователь, которому удалось вписать страницу в историю… криминалистики. Этим последователем был француз Альфонс Бертильон. Работавший помощником письмоводителя в полицейской префектуре Парижа, Бертильон был хорошо знаком с гипотезой Кетле, согласно которой строение тела человека является его индивидуальной характеристикой и что двух человек с совершенно одинаковыми антропологическими характеристиками быть не может. Гипотезу Кетле настойчивый Бертильон проверял на практике, измерив у большого числа заключенных парижских тюрем те самые антропологические параметры: окружность головы, длину ушей, длину ступней, ширину грудной клетки, рост и т.п.. В докладной записке, представленной Бертильоном префекту полиции в 1879 г., он отмечал, что, если взять одиннадцать антропологических параметров и занести их в карточку преступника, то вероятность их совпадения с такими же параметрами у другого преступника будет равна 1: 4 191 304. Если же мы внесем в карточку большее число антропологических параметров, то вероятность совпадения станет приблизительно в 70 раз меньше. Идея Бертильона состояла в систематизации карточек с данными антропологических параметров преступников – с тем, чтобы при задержании каждого нового преступника измерять его личные параметры и сверять их с картотекой. Только такой подход, по мнению Бертильона, исключит обманы и ошибки. Свой метод Бертильон противопоставлял обманчивой, по его словам фотографии… к тому же фотографии не поддавались, по его словам, столь же ясной систематизации.

В 1882 г. Бертильону было разрешено в порядке эксперимента проводить измерения и формировать специальную картотеку. К 15 февраля 1883 г. в картотеке было уже 1800 регистрационных карточек и в том же месяце задержанный преступник был опознан с помощью картотеки Бертильона. К нему пришла слава, и антропометрия по Бертильону – бертильонаж – стала широко известна и во Франции и за ее пределами. В 1888 г. Бертильон был назначен шефом вновь созданной полицейской службы идентификации города Парижа. События развивались и в том же году Лондонское королевское общество поручило Фрэнсису Гальтону подготовить на эту тему доклад.

Лорд Фрэнсис Гальтон (1822 - 1911) был широко известен многочисленными и разнообразными статистическими исследования девиз его был "Где возможно, считайте". Даже на своих лекциях Гальтон пытался определить – по количеству покашливаний слушателей - меру их внимательности. Во время прогулок собирал материал для «карты красоты» в Англии, подсчитывая количество очень красивых, заурядных и некрасивых женщин из встретившихся ему во время прогулки. Известно также, что однажды Гальтон пытался выяснить эффективность молитв. Для этого он, воспользовавшись соответствующими статистическими данными, сравнил частоты кораблекрушений для тех судов, на борту которых находились миссионеры и для тех, на борту которых миссионеров не было… Кузен и активный последователь великого Дарвина, Гальтон был широко известен в Англии своей любовью к антропологическим измерениям. Познакомившись с бертильонажем, Гальтон вспомнил про опубликованное в 1880 г. в Nature - ведущем научном журнале Англии – письмо врача Генри Фолдса. В этом письме Фолдс рассказывал о своем открытии абсолютной неповторимости узора капиллярных линий – пальцевого узора.

Перечитав письмо Фолдса и публикации других авторов, Гальтон понял, что стоит на пороге открытия. Проведя огромное количество измерений и разработав методы их классификации, обращаясь за консультацией к химикам, Гальтон выпускает в 1892 г. книгу "Отпечатки пальцев". Проходит еще десятилетие, и дактилоскопия становится признанным во всем мире методом идентификации преступников. В основе этого метода - установленный чисто статистически факт абсолютной индивидуальности узора капиллярных линий. Эта история отчетливо продемонстрировала практические возможности статистического метода; позже, в двадцатом столетии дактилоскопия приобрела статус самостоятельного раздела судебно-медицинской науки[3].

На уровень мировоззрения идея статистического, вероятностного знания была поднята знаменитым французским математиком Пьером Симоном Лапласом (1749 – 1827). В 1814 г. вышел в свет его ставший впоследствии знаменитым трактат «Опыт философии теории вероятностей». Лаплас считал, что существует Высший разум, обладающий абсолютным знанием. Человек же занимает промежуточное положение между Высшим разумом и незнанием и именно потому ему следует активно использовать теорию вероятностей. Лаплас глубоко убежден в том, что теория вероятностей обладает универсальной применимостью; некоторые его замечания мысли звучат – как станет ясно из последующего изложения – вполне современно. "…Мы так далеки от знания всех сил природы, что было бы мало научно отрицать явления только потому, что они необъяснимы при современном состоянии наших знаний. Мы должны только исследовать их с тем большим вниманием и тщательностью, чем нам кажется труднее допустить их; здесь-то становится необходимым исчисление вероятностей для того, чтобы определить, до каких пор следует умножать наблюдения или опыты, чтобы получить в пользу обнаружившихся в них сил вероятность, которая одержала бы верх над теми основаниями, на которых их все-таки можно бы не признавать".

Постепенно статистика получала признание и на институциональном уровне. В 1800 г. во Франции создано Генеральное бюро статистики. С 1834 г. в активном режиме работает Лондонское статистическое общество. Что касается России, то статистика народонаселения была включена в сферу интересов сначала Вольного экономического общества(1809),а впоследствии – Русского географического общества (1845). А первый международный статистический конгресс организовал в 1851 г. уже упоминавшийся выше бельгиец Кетле.

Вопросы к главе 1

1. Кому из ученых впервые удалось математически описать человеческое общество? Каков вклад статистики в соответствующую математическую модель?

2. Назовите имя ученого, проводившего аналогию между одним из институтов гражданского общества и одной из частей организма человека?

3. Кто и когда предложил философское обоснование необходимости для человека вероятностного знания? Как выглядело это обоснование?

4. Каким образом статистический подход позволил связать антропологию с криминалистикой?

5. Два экспериментатора проводят серию из 10 измерения, причем один из экспериментаторов сильно утомлен. Результаты их измерений описываются распределением Гаусса. У кого из экспериментаторов дисперсия распределения будет больше? Почему?

Вопрос от британских коллег. Пусть по вертикальной числовой оси отложено численное значение некоторого антропологического параметра, а по горизонтальной оси – число людей, характеризуемых именно таким значением параметра. Примером такого параметра может быть вес, рост, длина ступни, коэффициент интеллектуальности (IQ). Соответствующая кривая будет по форме соответствовать распределению Гаусса. Приведите примеры других антропологических параметров, которые распределены "по Гауссу". Какие антропологические параметры не подчиняются распределению Гаусса? Как, используя распределение Гаусса, вы бы могли графически описать возникновение мутаций?

Глава 2: на пути к микробной теории болезней

"Чем больше знаний и умений приобретает

медицина, тем меньше она возлагает надежд на полное очищение земли от болезнетворных микробов"

Станислав Лем.

Из сказанного следует, что первые применения статистики были связаны с гуманитарными науками (Граунт и Мальтус). Что же касается наук естественных, то принято считать, что статистика стала частью естественных науки благодаря распределениям Гаусса и Максвелла (распределение молекул идеального газа по скоростям). Весьма существенно, что в 19 в. к статистике обратились самые разные естественные науки, и в этом смысле она в некотором смысле выполнила роль объединяющего фактора для физики, математики и биологии. Российский историк науки Ю.В.Чайковский пишет в связи с этим об "идее равновозможности". Как можно определить "равновозможность"? Это философская идея, согласно которой все направления движения в мире равноправны, предпочтительных направлений движения не существует. Точно так же нет оснований говорить и о каких-то выделенных направлениях развития живых организмов, ни один вариант развития не может быть назван более предпочтительным по сравнению с другим. В физике идея равновозможности проявилась в идее равновероятности любых направлений движения молекул газа (именно это мы и имеем в виду, когда говорим, что молекулы газа движутся хаотически). В биологии – в положении о том, что мутации с равной вероятностью могут быть как положительными, так и отрицательными (в смысле их влияния на организм)" 1.

Фактически же, как мы увидим, в девятнадцатом веке статистические идеи начали проникать в естественные науки и «с другой стороны» - со стороны научного метода. В первую очередь этот процесс был связан с науками о живом. Ключевыми – в смысле подтверждения возможностей статистического подхода как научного метода - мы считаем историко-научные сюжеты, связанные с именами Джона Сноу и Игнаца Земмельвейса. Статистический подход обычно является начальным этапом изучения сложной системы; на этом этапе задача исследователя состоит в анализе поступающих к нему данных и выделении среди них главных и второстепенных. Повторим: под "статистическим подходом" мы имеем в виду не обработку данных в строгом соответствии с правилами математической статистики, но поиск корреляций(статистических зависимостей, когда с изменением одного параметра меняется другой).

Третий "биологический" сюжет касается процесса признания и распространения метода вакцинации Луи Пастера – роль статистиков была здесь также весьма важна.

Сюжет первый - открытие Джона Сноу. В изложении этой истории мы следуем учебнику Science for Public Understanding и материалам, размещенным на британском сайте www.scpub.org.

Как известно, первые заболевания холерой были зафиксированы в Индии приблизительно в 1817 г. В Европе эпидемии начались несколько позже…в Англии первые смерти от холеры были зафиксированы в 1831. В некоторых местностях Европы умирало более половины заболевших. И население, и политики и врачи были в панике, в некоторых местах врачи подвергались нападениям, из обвиняли в отравлении людей.

Что-то нужно было делать, но что? Первая модель возникновения заболевания основывалась на том, что процент заболевших был выше среди бедняков, живущих в перенаселенных кварталах. корреляции с плохими условиями жизни - и в первую очередь перенаселением (статистика неопровержимо свидетельствовала, что болезнь наиболее быстро распространялась именно в перенаселенных кварталах бедноты). Отсюда легко объяснить появление первой теории распространения холеры; несомненным ее достоинством была конкретная программа действий. Большинство докторов считали, что болезни подобные холере передаются или при контакте или через «испорченный воздух», эту теорию называли «миазменной». В 18 веке даже существовала практика определения характера болезни по специфическому запаху, исходящему от больного. Итак, ”миазменная теория” утверждала, что причиной заболевания являются запахи, а потому запах воспринимался как индикатор, позволяющий на уровне ощущений зафиксировать таинственный процесс распространения грозного заболевания. Томас Уэйкли, редактор авторитетного в медицинских кргуах журнала "Ланцет", следующим образом пытался в 1853 г. в редакционной статье ответить на вопрос “Что такое холера? “ “ … Она грибок, насекомое, нехватка озона, электрическое возмущение, миазм, Мы не знаем ничего, мы барахтаемся в водовороте догадок…»

"Миазменная теория" была весьма популярна в Европе приблизительно до середины девятнадцатого столетия. Именно эта теория стимулировала улучшение санитарного состояния больших городов (действия муниципальных властей должны быть направлены на снижение запахов). …в Лондоне, в частности, были установлены насосы, перекачивавшие канализационные отходы в Темзу.

Именно для борьбы с миазмами была построена первая канализация – с тем, чтобы убрать источники миазмов с городских улиц. Однако отходы жизнедеятельности попадали при этом в Темзу и становились причиной новых заболеваний. Можно сказать, что ориентация на неправильную теорию привела к негативным последствиям (хотя в целом рекомендации сторонников теории миазмов, несомненно, способствовали улучшению санитарного состояния городов).

Джон Сноу был врачом. Работать с холерными больными он начал в Ньюкастле и, после переезда в Лондон, продолжая лечить больных, начал собирать статистические данные о распространении холеры. При этом Сноу заметил, что процесс передачи заболевания от одного человека к другому занимает несколько дней. Именно этот факт привел его к гипотезе о существовании какого-то промежуточного переносчика заболевания. Трудно сказать, что побудило Сноу искать аргументы против теории миазмов, доказывать, что распространение холеры обусловлено контактом, а не миазмами. В общем-то гипотеза Сноу не пользовалась популярностью - по-видимому из-за того, что принятие этой гипотезы не раскрывало тайну распространения болезни. Кроме того, в Европе 18 – начале 19 веков запахи были неотъемлемым элементом городской среды и теория миазмов, связывавшая запахи с болезнями, была вполне естественной. Идея существования невидимого переносчика заболевания казалась поэтому чрезмерно абстрактной.

В 1849 г. Сноу опубликовал памфлет с изложением своей теории, согласно которой заболевание передавалось через воду, содержащую инфекционный агент, а также в непосредственном контакте. Вполне естественно, что Сноу противопоставлял свою теорию концепции "плохого воздуха". В это время большинство врачей не верили ему, и его памфлет был фактически проигнорирован. Действительно, "плохой воздух" был фактором, который стал существенным с ростом городского населения, а именно с ростом городского населения эпидемии холеры стали более интенсивными. Казалось, что запах может стать измеряемой характеристикой – правда, измерения не могли быть унифицированы, и все сводилось к субъективным ощущениям, но оставалась надежда, что в будущем соответствующие приборы удастся изобрести. К тому же корреляция между плохим воздухом и эпидемиями, несомненно, существовала, поскольку фактором эпидемий была плохая гигиена.

И именно на улучшение гигиены было направлено – в полном соответствии с теорией миазмов – строительство канализации в Лондоне. В целом появление канализации способствовало уменьшению масштаба эпидемий; в то же время именно появление канализации предоставило Сноу возможность со статистической достоверностью продемонстрировать, что вода является переносчиком заболевания. выявить позволило вывить улучшению …именно последствия этого строительства были выявлены Сноу в его статистических исследованиях, о которых мы сейчас и расскажем. К тому же запах – это объективная характеристика воздуха, регистрируемая органами обоняния.

В 1854 г., во время очередной и весьма сильной вспышки холеры в районе Лондона, расположенном близко к его собственному дому, Сноу обратил внимание на то, что количество заболевших было исключительно большим. Он посетил все дома, в которых были больные, и обнаружил, что все они пользовались водой из одного и того же насоса Broad pump. Жители того же района, но не пользовавшиеся водой из этого насоса, не заболели. В то же время заболели жители другого микрорайона Лондона, использовавшие воду из насоса Broad pump., он установил – исключительно на основе анализа статистических данных), что в пределах 300 метров от перекрестка Cambridge street и Broad street в течение 10 дней умерло 500 человек. Сопоставив дома, в которых они проживали, с картой районов Лондона, он увидел, что покупали питьевую воду в одном источнике – в насосе. Для Сноу это было подтверждением его идей… Сноу убедил власти закрыть доступ к насосу; вслед за этим смертность резко снизилась

Дата добавления: 2014-12-27