Следствие p-теоремы

Формулировка p-теоремы

Если общая функциональная зависимость вида (1) связывает n размерных величин, которые выражают через m основных единиц в системе СИ, то эта зависимость может быть сведена к уравнению подобия (2), содержащему i безразмерных величин

i = n – m, (4)

где i — число безразмерных величин;

n — число физических величин в (1);

m — число основных единиц в системе СИ, через
которые выражены эти величины.

Таблица 1

Основные первичные физические величины, символы,

размерности и единицы СИ

Величина	Единица СИ
Наименование	Обозна-чение	Раз-мерность	Наимено-вание	Обозначение
Между-нар.	На рус. яз.
Время	t	T	секунда	s	c
Длина	l	L	метр	m	м
Кол-во вещества	n	N	моль	mol	моль
Масса	m	M	килограмм	kg	кг
Сила света	J	J	канделла	kd	кд
Сила эл. тока	I	I	ампер	А	А
Температура	Т	Θ	кельвин	К	К

Если среди n физических величин в зависимости (1) имеется q неоднородных величин (т. е. величин с неоднородными размерностями), то количество симплексов S составляет

S = n – q, (5)

а количество комплексов К составляет

K = q – m. (6)

Здесь, как и в (4), m — количество основных единиц в системе СИ, установленной в настоящее время для научно-технической документации. Основные (независимые) единицы системы СИ приведены в табл. 1.

В отличие от основных, производные единицы системы СИ — это единицы производных величин, определяемые по уравнениям связи с единицами других величин.

Определим единицу измерения динамического коэффициента вязкости m, выразив его размерность сначала через производные, а затем основные единицы СИ:

[m] = Па·с = (H·м ^{– 2})·с = ((кг·м·с ^{– 2})·м ^{– 2})·с = кг·м^–1·с^–1.

Задача

Условие

Определить потери D Р давления на преодоление сопротивления трению изотермическим (Т = const) потоком вязкой несжимаемой жидкости в условиях установившегося ламинарного режима течения в круглой прямой горизонтальной трубе диаметром d на участке длиной l, если функциональная зависимость (1) имеет вид

D Р = D Р (m, w, d, l), (7)

где w — скорость потока.

Решение

1) Считаем количество n физических величин в зависимости (7).

n = 5.

2) Определяем количество основных единиц СИ, через
которые выражены эти величины, для чего выпишем формулы размерности каждой из величин в зависимости (7)

[D Р ] = Па = Н·м ^{– 2} = (кг·м·с ^{– 2})·м ^{– 2} = кг·м ^{– 1}·с ^{– 2} =

= [М·L ^{– 1}·T ^{– 2} ];

[m] = [M L ^{– 1} T ^{– 1}];

[ w ] = м·с ^{– 1} = [L·T ^{– 1}];

[ d ] = м = [L];

[ l ] = м = [L].

Следовательно, m = 3 (кг, м, с);

3) Определяем количество q величин с неодинаковой размерностью

q = 4, это D P, m, w, d.

4) Находим (4) ― число инвариантов в искомом уравнении подобия

i = n – m = 5 – 3 = 2.

В том числе:

количество симплексов согласно (5)

S = n – q = 5 – 4 = 1;

количество комплексов согласно (6)

K = q – m = 4 – 3 = 1.

5) Представим функциональную зависимость (7) в виде степенного уравнения

D Р = А m ^Bw^Cd^D l^E. (8)

6) Подставим формулы размерности физических величин
в степенное уравнение (8)

[ M^.L^–1.T^–2 ] = A [ M^.L^–1.T^–1 ] ^B. [ L^.T^–1 ] ^C. [ L ] ^{D .}[ L ] ^E. (9)

Раскрывая скобки в правой части последнего уравнения,
получим

[ M^.L^–1.T^–2 ] = A M^B.L^–B+C+D+E.T^–B–C. (10)

Поскольку А — безразмерный коэффициент, а размерности основных величин независимы, то для того чтобы полученное равенство удовлетворялось, необходимо равенство показателей степеней при одних и тех же единицах измерения в левой и правой частях уравнения (10).

Следовательно, для показателей степеней размерностей основных величин получим систему уравнений

[ M ] 1 = 1· B

[ L ] – 1 = (– 1)· B + 1· C + D + E (11)

[ T ] – 2 = (– 1)· B + (– 1)· C

Решая полученную систему уравнений (11), определяем значения показателей степеней

B = 1

C = 2 – B = 1

D = – 1 + B – C – E = – 1 – E.

6) Подставив в (8) эти значения показателей степеней,

получим

DР = A m w d ^–1 d ^{– E} l^E = A () ^E (12)

или в соответствии с (2)

p₁ (D Р) = А p₂ ^E,

где p₁ = , p₂ = = Г.

Зависимость из пяти физических величин приведена к зависимости безразмерных комплекса и симплекса. Полученный составной комплекс, состоит из произведения хорошо известных критериев подобия: Re и Eu.

С учетом этого критериальное уравнение имеет следующий вид:

Eu = A Re^–1 Г^Е (13)

π-теорема позволила получить наиболее рациональную форму обработки экспериментальных данных. Она позволила сгруппировать параметры и привести функциональную зависимость к безразмерному виду, тем самым снизив размерность задачи.

Последующая работа состоит в определении значений показателей степеней и безразмерного коэффициента А, которые находятся на основании опытных данных, как правило, экспериментально-статистическими методами.

Список рекомендуемой литературы

1. Алабужев П.М., Геронимус В.Б., Минкевич Л.М., Ше ховцов Б.А. /Теории подобия и размерностей. Моделирование/ Алабужев П.М., Геронимус В.Б., Минкевич Л.М., Шеховцов Б.А. —М.:Высшая школа, 1968. —206 с.

2. Романков П.Г., Курочкина М.И. /Гидромеханические
процессы химической технологии/ Романков П.Г., Курочкина М.И. — Л.: Химия, 1974. —288с.

3. Суфиянов Р.Ш., Горбенко О.О. /Элементы системного

анализа: учебное пособие для вузов/ Суфиянов Р.Ш.,

Горбенко О.О ― М.: МГУИЭ, 2009 ― 52 с.

Варианты заданий

Составить критериальные уравнения, если исходная функциональная зависимость имеет вид:

1. Δ P = f (ρ, w, d, l)

2. Δ P = f (ρ, μ, w, d, l)

3. Δ P = f (ρ, μ, w, g, d, l)

4. α = f (w, ρ, μ, λ, d)

5. α = f (w, ρ, μ, λ, c, d)

6. β = f (D, μ, ρ, l)

7. R = f (l, w, ρ, μ, g),

где

λ — коэффициент теплопроводности, Дж×м^–1×с^–1×град^–1,

Вт×м^–1×К^–1;

α — коэффициент теплоотдачи, Вт×м^–2×К^–1;

c — удельная теплоёмкость, Дж×кг^–1×К^–1;

μ — коэффициент динамической вязкости, Па×с;

ρ — плотность, кг×м^–3;

β — коэффициент массоотдачи, м×с^–1;

D — коэффициент диффузии, м²×с^–1;

g — ускорение свободного падения, м×с^–2;

R — сила сопротивления, Н.

Число Прандтля ,

число Нуссельта ,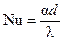

число Фруда ,

диффузионное число Нуссельта

диффузионное число Прандтля

Дата добавления: 2014-12-27