Метода линейного программирования

Практическое применение

Математические методы оптимизации относятся к классу
условных экстремальных задач. Внешне эти методы отличаются от постановки обычных задач поиска экстремума функции лишь тем, что здесь экстремум отыскивают при некоторых ограничениях, условиях. Такими ограничениями в этих задачах служат уравнения математической модели системы. Все методы оптимизации можно разделить на аналитические и численные.

Для относительно небольшой части инженерных задач, к которым применимы аналитические решения, чаще всего с целью оптимизации применяют метод неопределенных множителей Лагранжа. Сущность метода заключается в использовании функции Лагранжа, позволяющей перевести задачу из класса условных экстремальных задач в класс безусловных (метод поиска экстремума функции).

Большинство задач оптимизации сводятся к численным методам. К ним относятся задачи линейного и нелинейного программирования.

К линейному программированию относятся задачи оптимизации, когда как ограничения, налагаемые на параметры, так и выражение для критерия оптимальности являются линейными функциями.

В качестве ограничений можно использовать уравнения математической модели объекта.

Оптимальным значением параметра называют такое его значение, при котором некоторая вспомогательная функция
(критерий оптимальности) достигает экстремального значения.

Задачи оптимизации — это условные экстремальные задачи, в которых находят экстремум при некоторых ограничениях (условиях).

Задача оптимизации считается задачей линейного программирования, если:

1) критерий оптимальности Р (целевая функция, показатель эффективности) есть линейная функция от параметров

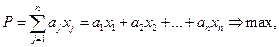(20)

где a_j — заданные коэффициенты, j = 1...n;

х_j – параметры, j = 1...n.

2) ограничительные условия, налагаемые на параметры,
имеют вид линейных равенств (или неравенств, которые можно привести к равенствам):

1-е ограничение: a ₁₁ x ₁ + a ₁₂ x ₂ +... + a _{1 n} x_n = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ +... + a _{2 n} x_n = b ₂ (21)

m -е ограничение: a_{m 1} x ₁ + a_{m 2} x ₂ +... + a_mnx_n = b_m.

где n — число параметров (переменных) х_j,

m — число ограничений.

Эти условия справедливы только в том случае, если

х_j ³ 0. (22)

Уравнение (20) и система уравнений (21) при условии (22) представляют стандартную форму, или основную задачу линейного программирования:

Найти неотрицательные значения параметров х_j (22), которые удовлетворяли бы ограничениям-равенствам (21) и обращали в максимум функцию (20).

Задача линейного программирования имеет смысл и бес-конечное множество решений только в том случае, когда число неизвестных (число параметров) больше числа ограничений: (n – m) 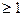, т.е. в оптимизационных задачах число переменных всегда больше числа ограничений.

Задача

Критерий оптимальности задан в следующем виде:

Р = x ₁ + x ₂ Þ max.

Ограничительные условия, налагаемые на параметры, заданы неравенствами:

0,2 х ₁ + 0,1 х ₂ £ 0,1

(23)

0,1 х ₁ + 0,2 х ₂ £ 0,1.

Найти, при каких оптимальных значениях параметров х ₁ и х ₂ критерий оптимальности Р будет максимальным.

Решение

Переведем исходные неравенства в равенства. Для этого необходимо ввести дополнительные переменные х ₃ и х ₄.

В результате получим систему уравнений 1*, 2* с числом уравнений (ограничений) m = 2 и числом неизвестных параметров n = 4, при условии, х_j :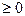

0,2 х ₁ + 0,1 х ₂ + х ₃ = 0,1 (1*)

(24)

0,1 х ₁ + 0,2 х ₂ + х ₄ = 0,1. (2*)

Эту задачу линейного программирования можно решать аналитическим или графическим способом.

Графическое решение задачи

На фазовой плоскости переменных х ₁, х ₂ представим
область допустимых решений (ОДР) основной задачи линейного программирования, ограниченную условиями (23), или, что то же самое (24), при х ₃ = х ₄ = 0, х_j ≥ 0.

Запишем систему уравнений (19) в более удобном виде:

2 х ₁ + х ₂ +10 х ₃ = 1 (1*)

(25)

х ₁ +2 х ₂ + 10 х ₄ = 1. (2*)

Построим прямые, соответствующие этим уравнениям:

1) Из (1*) имеем: х ₃ = 0; 2 х ₁ + х ₂ = 1; х ₂ = 1 – 2 х ₁.

Координаты точек для построения прямой: х ₂ = 0, х ₁ = 0,5
и х ₁ = 0, х ₂ = 1.

2) Из (2*): х ₄ = 0; х ₁ + 2 х ₂ = 1; х ₁ = 1 – 2 х ₂.

Координаты точек для построения прямой: х ₁ = 0, х ₂ = 0,5
и х ₂ = 0, х ₁ = 1.

Проведем прямые и обозначим вершины четырехугольника: А, B, C, D.

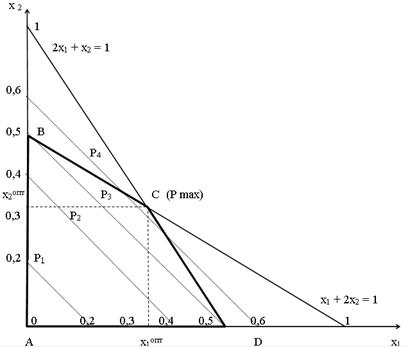
Рис. 1. Графическое решение задачи

3) Далее необходимо рассмотреть целевую функцию:

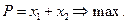
Имеем: х ₁ = Р – х ₂.

4)В пределах ОДР проведем линию, отвечающую произвольно выбранному значению функции. Допустим, Р ₁ = 0,2. Эта линия называется изолинией, линией постоянства критерия оптимальности.

Координаты точек: х ₂ = 0, х ₁ = 0,2; х ₁= 0, х ₂ = 0,2.

5)Зададим Р ₂ = 0,4 и построим следующую изолинию.

6)Зададим Р ₃ = 0,5 и построим третью изолинию.

Очевидно, что целевая функция возрастает и, если передвигать изолинии дальше, мы увидим: одна из этих изолиний (Р ₄) пройдёт через вершину С В этой точке и будет максимальное значение целевой функции: х ₁ = 1/3 = 0,333, x ₂ = 1/3

Рис. 7. Графическое решение задачи

Область ABCD, в которой находятся неотрицательные значения параметров, и будет областью допустимых решений (ОДР) (рис. 7).

3) Далее необходимо рассмотреть целевую функцию

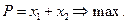
Выразим х ₁ = Р – х ₂.

4) В пределах ОДР проведем линию, соответствующую произвольно выбранному значению функции. Допустим, Р ₁= 0,2. Эта линия называется изолинией, линией постоянства критерия оптимальности.

Координаты точек: х ₂ = 0, х ₁ = 0,2; х ₁= 0, х ₂ = 0,2.

5) Зададим Р ₂ = 0,4 и построим следующую изолинию.

6) Зададим Р ₃ = 0,5 и построим третью изолинию.

Очевидно, что целевая функция возрастает и если передвигать изолинии дальше, то одна из них (Р ₄) пройдёт через вершину С. В этой точке и будет максимальное значение целевой функции: х ₁ = 1/3 = 0,333, x ₂ = 1/3 = 0,333 при Р = 2/3= 0,666.

Аналитическое решение задачи

Аналитическое решение задачи получают перебором
базисных решений.

Пусть математическая модель содержит m независимых
линейных уравнений, включающих n параметров (режимных
и конструктивных): x ₁, x ₂, …, x_n. В задачах оптимизации n > m, а разность k =n – m определяет число свободных (варьируемых) параметров. Если из числа n параметров зафиксировать любые k параметров, принятых в качестве свободных, то систему уравнений можно разрешить однозначно. Решения, где свободные переменные приравниваются нулю, а другие переменные, из n параметров, принимают неотрицательные значения, называются базисными решениями. Решение задачи линейного программирования лежит в базисной области.

Исходная система уравнений имеет ограниченное множество базисных решений. Например, в данном случае при n = 4, m = 2 и k = 4 – 2 = 2 существуют следующие шесть базисных решений: х ₁=0, х ₂=0; х ₁=0, х ₃=0; х ₁=0, х ₄=0; х ₂=0, х ₃=0; х ₂=0, х ₄=0; х ₃=0, х ₄=0.

Доказано, что оптимальное решение в задачах линейного программирования следует искать среди базисных решений. Поиск проводят перебором всех базисных решений для
выбора из всех параметров х одного параметра — с экстремальным значением критерия оптимальности.

Таблица 5

Свободные переменные	Базисные переменные	ПЭ P = x 1 + x 2
x 1 = 0	x 2 = 0	x 3 = 1/10	x 4 = 1/10	Р = 0
x 1 = 0	x 3 = 0	x 2 = 1	x 4 =­ - 1/10	Р = 1
x 1 = 0	x 4 = 0	x 2 = 1/2	x 3 = 1/20	Р = 1/2
x 2 = 0	x 3 = 0	x 1 = 1/2	x 4 = 1/20	F = 1/2
x 2 = 0	x 4 = 0	x 1 = 1	x 3 = - 1/10	Р = 1
x 3 = 0	x 4 = 0	x 1 = 1/3	x 2 = 1/3	Р = 2/3

Список рекомендуемой литературы

1. Кузнецов Ю.Н., Кузубов В.И., Валощенко А.Б. /Математическое программирование/ Кузнецов Ю.Н., Кузубов В.И., Валощенко А.Б — М.: Высшая школа, 1976. 352с.

2. Ларин Р. М., Плясунов А. В., Пяткин А. В. /Методы оптимизации. Примеры и задачи: учебное пособие/ Ларин Р. М., Плясунов А. В., Пяткин А. В. —Новосибирск: Новосибирский государственный университет, 2003. 120 с.

3. Суфиянов Р.Ш., Горбенко О.О. /Элементы системного

анализа: учебное пособие для вузов/ Суфиянов Р.Ш.,

Горбенко О.О ― М.: МГУИЭ, 2009 ― 52 с.

Варианты заданий

Дата добавления: 2014-12-27